120-gon
| Regular 120-gon | |
|---|---|
 A regular 120-gon | |
| Type | Regular polygon |
| Edges and vertices | 120 |
| Schläfli symbol | {120}, t{60}, tt{30}, ttt{15} |
| Coxeter diagram |
|
| Symmetry group | Dihedral (D120), order 2×120 |
| Internal angle (degrees) | 177° |
| Dual polygon | Self |
| Properties | Convex, cyclic, equilateral, isogonal, isotoxal |
In geometry, a 120-gon is a polygon with 120 sides. The sum of any 120-gon's interior angles is 21240 degrees.
Alternative names include dodecacontagon and hecatonicosagon.[1]
Regular 120-gon properties
A regular 120-gon is represented by Schläfli symbol {120} and also can be constructed as a truncated hexacontagon, t{60}, or a twice-truncated triacontagon, tt{30}, or a thrice-truncated pentadecagon, ttt{15}.
One interior angle in a regular 120-gon is 177°, meaning that one exterior angle would be 3°.
The area of a regular 120-gon is (with t = edge length)
and its inradius is
The circumradius of a regular 120-gon is
This means that the trigonometric functions of π/120 can be expressed in radicals.
Constructible
Since 120 = 23 × 3 × 5, a regular 120-gon is constructible using a compass and straightedge.[2] As a truncated hexacontagon, it can be constructed by an edge-bisection of a regular hexacontagon.
Symmetry
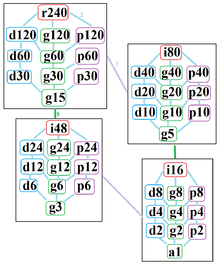
The regular 120-gon has Dih120 dihedral symmetry, order 240, represented by 120 lines of reflection. Dih120 has 15 dihedral subgroups: (Dih60, Dih30, Dih15), (Dih40, Dih20, Dih10, Dih5), (Dih24, Dih12, Dih6, Dih3), and (Dih8, Dih4, Dih2, Dih1). And 16 more cyclic symmetries: (Z120, Z60, Z30, Z15), (Z40, Z20, Z10, Z5), (Z24, Z12, Z6, Z3), and (Z8, Z4, Z2,Z1), with Zn representing π/n radian rotational symmetry.
These 32 symmmetries are related to 44 distinct symmetries on the 120-gon. John Conway labels these lower symmetries with a letter and order of the symmetry follows the letter.[3] He gives d (diagonal) with mirror lines through vertices, p with mirror lines through edges (perpendicular), i with mirror lines through both vertices and edges, and g for rotational symmetry. a1 labels no symmetry.
These lower symmetries allows degrees of freedom in defining irregular 120-gons. Only the g120 symmetry has no degrees of freedom but can seen as directed edges.
120-gram
A 120-gram is a 120-sided star polygon. There are 15 regular forms given by Schläfli symbols {120/7}, {120/11}, {120/13}, {120/17}, {120/19}, {120/23}, {120/29}, {120/31}, {120/37}, {120/41}, {120/43}, {120/47}, {120/49}, {120/53}, and {120/59}, as well as 44 compound star figures with the same vertex configuration.
| Picture |  {120} |
 {120/7} |
 {120/11} |
 {120/13} |
 {120/17} |
 {120/19} |
 {120/23} |
 {120/29} |
|---|---|---|---|---|---|---|---|---|
| Interior angle | 177° | 159° | 147° | 141° | 129° | 123° | 111° | 93° |
| Picture |  {120/31} |
 {120/37} |
 {120/41} |
 {120/43} |
 {120/47} |
 {120/49} |
 {120/53} |
 {120/59} |
| Interior angle | 87° | 69° | 57° | 51° | 39° | 33° | 21° | 3° |
References
- ↑ Norman Johnson, Geometries and Transformations (2015), Chapter 11, section 11.5 Spherical Coxeter groups, 11.5.5 full polychoric groups
- ↑ Constructible Polygon
- ↑ John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, (2008) The Symmetries of Things, ISBN 978-1-56881-220-5 (Chapter 20, Generalized Schaefli symbols, Types of symmetry of a polygon pp. 275-278)