Octacontagon
| Regular octacontagon | |
|---|---|
 A regular octacontagon | |
| Type | Regular polygon |
| Edges and vertices | 80 |
| Schläfli symbol | {80}, t{40}, tt{20}, ttt{10}, tttt{5} |
| Coxeter diagram |
|
| Symmetry group | Dihedral (D80), order 2×80 |
| Internal angle (degrees) | 175.5° |
| Dual polygon | Self |
| Properties | Convex, cyclic, equilateral, isogonal, isotoxal |
In geometry, an octacontagon (or ogdoëcontagon or 80-gon from Ancient Greek ὁγδοήκοντα, eighty[1]) is an eighty-sided polygon.[2][3] The sum of any octacontagon's interior angles is 14040 degrees.
Regular octacontagon
A regular octacontagon is represented by Schläfli symbol {80} and can also be constructed as a truncated tetracontagon, t{40}, or a twice-truncated icosagon, tt{20}, or a thrice-truncated decagon, ttt{10}, or a four-fold-truncated pentagon, tttt{5}.
One interior angle in a regular octacontagon is 175 1⁄2°, meaning that one exterior angle would be 4 1⁄2°.
The area of a regular octacontagon is (with t = edge length)
and its inradius is
The circumradius of a regular octacontagon is
Construction
Since 80 = 24 × 5, a regular octacontagon is constructible using a compass and straightedge.[4] As a truncated tetracontagon, it can be constructed by an edge-bisection of a regular tetracontagon. This means that the trigonometric functions of π/80 can be expressed in radicals:
Symmetry
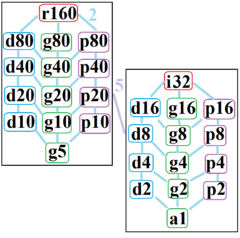
The regular octacontagon has Dih80 dihedral symmetry, order 80, represented by 80 lines of reflection. Dih40 has 9 dihedral subgroups: (Dih40, Dih20, Dih10, Dih5), and (Dih16, Dih8, Dih4, and Dih2, Dih1). It also has 10 more cyclic symmetries as subgroups: (Z80, Z40, Z20, Z10, Z5), and (Z16, Z8, Z4, Z2, Z1), with Zn representing π/n radian rotational symmetry.
John Conway labels these lower symmetries with a letter and order of the symmetry follows the letter.[5] r160 represents full symmetry and a1 labels no symmetry. He gives d (diagonal) with mirror lines through vertices, p with mirror lines through edges (perpendicular), i with mirror lines through both vertices and edges, and g for rotational symmetry.
These lower symmetries allows degrees of freedoms in defining irregular octacontagons. Only the g80 subgroup has no degrees of freedom but can seen as directed edges.
Octacontagram
An octacontagram is an 80-sided star polygon. There are 15 regular forms given by Schläfli symbols {80/3}, {80/7}, {80/9}, {80/11}, {80/13}, {80/17}, {80/19}, {80/21}, {80/23}, {80/27}, {80/29}, {80/31}, {80/33}, {80/37}, and {80/39}, as well as 24 regular star figures with the same vertex configuration.
| Picture |  {80/3} |
 {80/7} |
 {80/9} |
 {80/11} |
 {80/13} |
 {80/17} |
 {80/19} |
 {80/21} |
|---|---|---|---|---|---|---|---|---|
| Interior angle | 166.5° | 148.5° | 139.5° | 130.5° | 121.5° | 103.5° | 94.5° | 85.5° |
| Picture |  {80/23} |
 {80/27} |
 {80/29} |
 {80/31} |
 {80/33} |
 {80/37} |
 {80/39} |
|
| Interior angle | 76.5° | 58.5° | 49.5° | 40.5° | 31.5° | 13.5° | 4.5° |
References
- ↑ Greek Numbers and Numerals (Ancient and Modern) by Harry Foundalis
- ↑ Gorini, Catherine A. (2009), The Facts on File Geometry Handbook, Infobase Publishing, p. 110, ISBN 9781438109572.
- ↑ The New Elements of Mathematics: Algebra and Geometry by Charles Sanders Peirce (1976), p.298
- ↑ Constructible Polygon
- ↑ The Symmetries of Things, Chapter 20