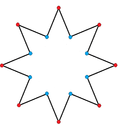
Octagram
| Regular octagram | |
|---|---|
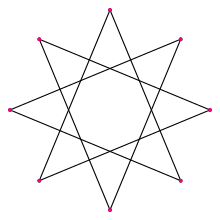 A regular octagram | |
| Type | Regular star polygon |
| Edges and vertices | 8 |
| Schläfli symbol |
{8/3} t{4/3} |
| Coxeter diagram |
|
| Symmetry group | Dihedral (D8) |
| Internal angle (degrees) | 45° |
| Dual polygon | self |
| Properties | star, cyclic, equilateral, isogonal, isotoxal |
In geometry, an octagram is an eight-angled star polygon.
The name octagram combine a Greek numeral prefix, octa-, with the Greek suffix -gram. The -gram suffix derives from γραμμή (grammḗ) meaning "line".[1]
Detail
In general, an octagram is any self-intersecting octagon (8-sided polygon).
The regular octagram is labeled by the Schläfli symbol {8/3}, which means an 8-sided star, connected by every third point.
Variations
These variations have a lower dihedral, Dih4, symmetry:
 Narrow 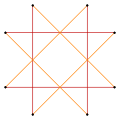 Wide (45 degree rotation) |
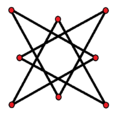  Isotoxal |
 An old Flag of Chile contained this octagonal star geometry with edges removed. |
 The geometry can be adjusted so 3 edges cross at a single point, like the Auseklis symbol |
 An 8-point compass rose can be seen as an octagonal star, with 4 primary points, and 4 secondary points. |
The symbol Rub el Hizb is a Unicode glyph ۞ at U+06DE.
As a quasitruncated square
Deeper truncations of the square can produce isogonal (vertex-transitive) intermediate star polygon forms with equal spaced vertices and two edge lengths. A truncated square is an octagon, t{4}={8}. A quasitruncated square, inverted as {4/3}, is an octagram, t{4/3}={8/3}.[2]
The uniform star polyhedron stellated truncated hexahedron, t'{4,3}=t{4/3,3} has octagram faces constructed from the cube in this way.
| Regular | Quasiregular | Isogonal | Quasiregular |
|---|---|---|---|
 {4} |
 t{4}={8} |
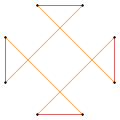 |
 t'{4}=t{4/3}={8/3} |
| Regular | Uniform | Isogonal | Uniform |
 {4,3} |
 t{4,3} |
 |
 t'{4,3}=t{4/3,3} |
Star polygon compounds
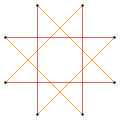
There are two regular octagrammic star figures (compounds) of the form {8/k}, the first constructed as two squares {8/2}=2{4}, and second as four degenerate digons, {8/4}=4{2}. There are other isogonal and isotoxal compounds including rectangular and rhombic forms.
| Regular | Isogonal | Isotoxal | ||
|---|---|---|---|---|
.svg.png) a{8}={8/2}=2{4} |
.svg.png) {8/4}=4{2} |
 |
 |
 |
Other presentations of an octagonal star
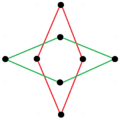
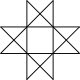
An octagonal star can be seen as a concave hexadecagon, with internal intersecting geometry erased. It can also be dissected by radial lines.
| 2{4} | 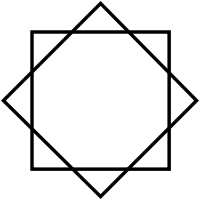 |
 |
 |
 |
|---|---|---|---|---|
| {8/3} |  |
 |
 |
 |
 |
 |
 |
 | |
 |
 |
 |
 |
See also
- Usage
- Rub el Hizb - Islamic character
- Star of Lakshmi - Indian character
- Auseklis – usage of regular octagram by Latvians
- Guñelve – representation of Venus in Mapuche iconography.
- Selburose – usage of regular octagram in Norwegian design
- Stars generally
References
- ↑ γραμμή, Henry George Liddell, Robert Scott, A Greek-English Lexicon, on Perseus
- ↑ The Lighter Side of Mathematics: Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and its History, (1994), Metamorphoses of polygons, Branko Grünbaum
- Grünbaum, B. and G.C. Shephard; Tilings and Patterns, New York: W. H. Freeman & Co., (1987), ISBN 0-7167-1193-1.
- Grünbaum, B.; Polyhedra with Hollow Faces, Proc of NATO-ASI Conference on Polytopes ... etc. (Toronto 1993), ed T. Bisztriczky et al., Kluwer Academic (1994) pp. 43–70.
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 26. pp. 404: Regular star-polytopes Dimension 2)
