Tetracontaoctagon
| Regular tetracontaoctagon | |
|---|---|
 A regular tetracontaoctagon | |
| Type | Regular polygon |
| Edges and vertices | 48 |
| Schläfli symbol | {48}, t{24}, tt{12}, ttt{6}, tttt{3} |
| Coxeter diagram |
|
| Symmetry group | Dihedral (D48), order 2×48 |
| Internal angle (degrees) | 172.5° |
| Dual polygon | Self |
| Properties | Convex, cyclic, equilateral, isogonal, isotoxal |
In geometry, a tetracontaoctagon (or tetracontakaioctagon) or 48-gon is a forty-eight sided polygon. The sum of any tetracontaoctagon's interior angles is 8280 degrees.
Regular tetracontaoctagon
The regular tetracontaoctagon is represented by Schläfli symbol {48} and can also be constructed as a truncated icositetragon, t{24}, or a twice-truncated dodecagon, tt{12}, or a thrice-truncated hexagon, ttt{6}, or a fourfold-truncated triangle, tttt{3}.
One interior angle in a regular tetracontaoctagon is 172 1⁄2°, meaning that one exterior angle would be 7 1⁄2°.
The area of a regular tetracontaoctagon is: (with t = edge length)
The tetracontaoctagon appeared in Archimedes' polygon approximation of pi, along with the hexagon (6-gon), dodecagon (12-gon), icositetragon (24-gon), and enneacontahexagon (96-gon).
Construction
Since 48 = 24 × 3, a regular tetracontaoctagon is constructible using a compass and straightedge.[1] As a truncated icositetragon, it can be constructed by an edge-bisection of a regular icositetragon.
Symmetry
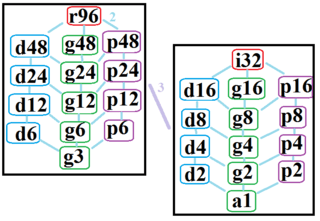
The regular tetracontaoctagon has Dih48 symmetry, order 96. There are nine subgroup dihedral symmetries: (Dih24, Dih12, Dih6, Dih3), and (Dih16, Dih8, Dih4, Dih2 Dih1), and 10 cyclic group symmetries: (Z48, Z24, Z12, Z6, Z3), and (Z16, Z8, Z4, Z2, Z1).
These 20 symmetries can be seen in 28 distinct symmetries on the tetracontaoctagon. John Conway labels these by a letter and group order.[2] The full symmetry of the regular form is r96 and no symmetry is labeled a1. The dihedral symmetries are divided depending on whether they pass through vertices (d for diagonal) or edges (p for perpendiculars), and i when reflection lines path through both edges and vertices. Cyclic symmetries in the middle column are labeled as g for their central gyration orders.
Each subgroup symmetry allows one or more degrees of freedom for irregular forms. Only the g48 subgroup has no degrees of freedom but can seen as directed edges.
Tetracontaoctagram
A tetracontaoctagram is a 48-sided star polygon. There are seven regular forms given by Schläfli symbols {48/5}, {48/7}, {48/11}, {48/13}, {48/17}, {48/19}, and {48/23}, as well as 16 compound star figures with the same vertex configuration.
| Picture |  {48/5} |
 {48/7} |
 {48/11} |
 {48/13} |
 {48/17} |
 {48/19} |
 {48/23} |
|---|---|---|---|---|---|---|---|
| Interior angle | 142.5° | 127.5° | 97.5° | 82.5° | 52.5° | 37.5° | 7.5° |
References
- ↑ Constructible Polygon
- ↑ John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, (2008) The Symmetries of Things, ISBN 978-1-56881-220-5 (Chapter 20, Generalized Schaefli symbols, Types of symmetry of a polygon pp. 275-278)