Enneagram (geometry)
| Enneagram | |
|---|---|
 Enneagrams shown as sequential stellations | |
| Edges and vertices | 9 |
| Symmetry group | Dihedral (D9) |
| Internal angle (degrees) |
100° {9/2} 20° {9/4} |
In geometry, an enneagram is a nine-pointed plane figure. It is sometimes called a nonagram.
The name enneagram combines the numeral prefix, ennea-, with the Greek suffix -gram. The -gram suffix derives from γραμμῆς (grammēs) meaning a line.[1]
Regular enneagram
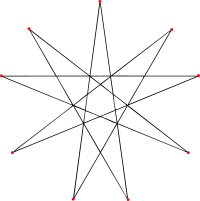
A regular enneagram (a nine-sided star polygon) is constructed using the same points as the regular enneagon but connected in fixed steps. It has two forms, represented by a Schläfli symbol as {9/2} and {9/4}, connecting every second and every fourth points respectively.
There is also a star figure, {9/3} or 3{3}, made from the regular enneagon points but connected as a compound of three equilateral triangles.[2][3] (If the triangles are alternately interlaced, this results in a Brunnian link.) This star figure is sometimes known as the star of Goliath, after {6/2} or 2{3}, the star of David.[4]
This geometrical figure should not be confused with the logic puzzles called nonograms.
| Compound | Regular star | Regular compound |
Regular star |
|---|---|---|---|
 Complete graph K9 |
 {9/2} |
.svg.png) {9/3} or 3{3} |
 {9/4} |
Other enneagram figures
 The final stellation of the icosahedron has 2-isogonal enneagram faces. It is a 9/4 wound star polyhedron, but the vertices are not equally spaced. |
 The Fourth Way teachings and the Enneagram of Personality use an irregular enneagram consisting of a triangle and an irregular hexagram. |
 The Bahá'í nine-pointed star |
The nine-pointed star or enneagram can also symbolize the nine gifts or fruits of the Holy Spirit.[5]
In popular culture
- The heavy metal band Slipknot uses the {9/3} star figure enneagram as a symbol.[6]
See also
- Nonagon (enneagon)
- List of regular star polygons
References
- ↑ γραμμή, Henry George Liddell, Robert Scott, A Greek-English Lexicon, on Perseus
- ↑ Grünbaum, B. and G.C. Shephard; Tilings and Patterns, New York: W. H. Freeman & Co., (1987), ISBN 0-7167-1193-1.
- ↑ Grünbaum, B.; Polyhedra with Hollow Faces, Proc of NATO-ASI Conference on Polytopes ... etc. (Toronto 1993), ed T. Bisztriczky et al., Kluwer Academic (1994) pp. 43-70.
- ↑ Weisstein, Eric W. "Nonagram". From MathWorld – A Wolfram Web Resource. http://mathworld.wolfram.com/Nonagram.html
- ↑ Our Christian Symbols by Friedrich Rest (1954), ISBN 0-8298-0099-9, page 13.
- ↑ Slipknot Nonagram
Bibliography
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 26. pp. 404: Regular star-polytopes Dimension 2)