Tetrahedrally diminished dodecahedron
| Dorman Luke self-dual form | |
|---|---|
 | |
| Tetrahedrally stellated icosahedron | |
 | |
| Tetrahedrally diminished dodecahedron | |
 | |
| Conway polyhedron notation | pT |
| Faces | 16: 4 {3} + 12 quadrilaterals |
| Edges | 30 |
| Vertices | 16 |
| Vertex configuration | 3.4.4.4 4.4.4 |
| Symmetry group | T, [3,3]+, (332), order 12 |
| Dual polyhedron | Self-dual |
| Properties | convex |
   Nets | |
In geometry, a tetrahedrally diminished[1] dodecahedron (also tetrahedrally stellated icosahedron) is a topologically self-dual polyhedron made of 16 vertices, 30 edges, and 16 faces (4 equilateral triangles and 12 identical quadrilaterals).[2]
It has chiral tetrahedral symmetry, and so its geometry can be constructed from pyritohedral symmetry of the pseudoicosahedron with 4 faces stellated, or from the pyritohedron, with 4 vertices diminished. Within its tetrahedral symmetry, it has geometric varied proportions. By Dorman Luke dual construction, a unique geometric proportion can be defined. The kite faces have edges of length ratio ~ 1:0.6325.
As a self-dual hexadecahedron, it is one of 302404 forms, 1476 with at least order 2 symmetry, and the only one with tetrahedral symmetry.[3]
As a diminished regular dodecahedron, with 4 vertices removed, the quadrilaterals faces are trapezoids.
As a stellation of the regular icosahedron it is one of 32 stellations defined with tetrahedral symmetry. It has kite faces.[4]
In Conway polyhedron notation, it can represented as pT, applying George W. Hart's propeller operator to a regular tetrahedron.[5]
Related polytopes and honeycombs
This polyhedron represents the vertex figure of a hyperbolic uniform honeycomb, the partially diminished icosahedral honeycomb, pd{3,5,3}, with 12 pentagonal antiprisms and 4 dodecahedron cells meeting at every vertex.
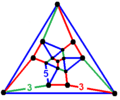
- Vertex figure projected as Schlegel diagram
References
- ↑ It is also less accurately called a tetrahedrally truncated dodecahedron
- ↑ Tetrahedrally Stellated Icosahedron
- ↑ Self-Dual Hexadecahedra
- ↑ Tetrahedral Stellations of the Icosahedron
- ↑ Conway Notation for Polyhedra
External links
- tetrahedrally truncated dodecahedron and stellated icosahedron
- Generation of an icosahedron by the intersection of five tetrahedra: geometrical and crystallographic features of the intermediate polyhedra
- VRML model as truncated regular dodecahedron
- VRML model as tetrahedrally stellated icosahedron