Myriagon
| Regular myriagon | |
|---|---|
 A regular myriagon | |
| Type | Regular polygon |
| Edges and vertices | 10000 |
| Schläfli symbol | {10000}, t{5000}, tt{2500}, ttt{1250}, tttt{625} |
| Coxeter diagram |
|
| Symmetry group | Dihedral (D10000), order 2×10000 |
| Internal angle (degrees) | 179.964° |
| Dual polygon | Self |
| Properties | Convex, cyclic, equilateral, isogonal, isotoxal |
In geometry, a myriagon or 10000-gon is a polygon with 10000 sides . Several philosophers have used the regular myriagon to illustrate issues regarding thought.[1][2][3][4][5]
Regular myriagon
A regular myriagon is represented by Schläfli symbol {10000} and can be constructed as a truncated 5000-gon, t{5000}, or a twice-truncated 2500-gon, tt{2500}, or a thrice-truncaed 1250-gon, ttt{1250), or a four-fold-truncated 625-gon, tttt{625}.
The measure of each internal angle in a regular myriagon is 179.964°. The area of a regular myriagon with sides of length a is given by
The result differs from the area of its circumscribed circle by up to 40 parts per billion.
Because 10000 = 24 × 54, the number of sides is neither a product of distinct Fermat primes nor a power of two. Thus the regular myriagon is not a constructible polygon. Indeed, it is not even constructible with the use of neusis or an angle trisector, as the number of sides is neither a product of distinct Pierpont primes, nor a product of powers of two and three.
Symmetry
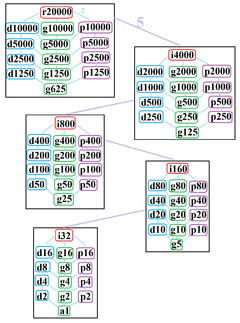
The regular myriagon has Dih10000 dihedral symmetry, order 20000, represented by 10000 lines of reflection. Dih100 has 24 dihedral subgroups: (Dih5000, Dih2500, Dih1250, Dih625), (Dih2000, Dih1000, Dih500, Dih250, Dih125), (Dih400, Dih200, Dih100, Dih50, Dih25), (Dih80, Dih40, Dih20, Dih10, Dih5), and (Dih16, Dih8, Dih4, Dih2, Dih1). It also has 25 more cyclic symmetries as subgroups: (Z10000, Z5000, Z2500, Z1250, Z625), (Z2000, Z1000, Z500, Z250, Z125), (Z400, Z200, Z100, Z50, Z25), (Z80, Z40, Z20, Z10), and (Z16, Z8, Z4, Z2, Z1), with Zn representing π/n radian rotational symmetry.
John Conway labels these lower symmetries with a letter and order of the symmetry follows the letter.[6] r20000 represents full symmetry, and a1 labels no symmetry. He gives d (diagonal) with mirror lines through vertices, p with mirror lines through edges (perpendicular), i with mirror lines through both vertices and edges, and g for rotational symmetry.
These lower symmetries allows degrees of freedom in defining irregular myriagons. Only the g10000 subgroup has no degrees of freedom but can seen as directed edges.
Myriagram
A myriagram is an 10000-sided star polygon. There are 1999 regular forms[7] given by Schläfli symbols of the form {10000/n}, where n is an integer between 2 and 5000 that is coprime to 10000. There are also 3000 regular star figures in the remaining cases.
See also
References
- ↑ Meditation VI by Descartes (English translation).
- ↑ Hippolyte Taine, On Intelligence: pp. 9–10
- ↑ Jacques Maritain, An Introduction to Philosophy: p. 108
- ↑ Alan Nelson (ed.), A Companion to Rationalism: p. 285
- ↑ Paolo Fabiani, The philosophy of the imagination in Vico and Malebranche: p. 222
- ↑ The Symmetries of Things, Chapter 20
- ↑ 5000 cases - 1 (convex) - 1000 (multiples of 5) - 2500 (multiples of 2)+ 500 (multiples of 2 and 5)