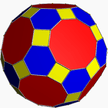
Truncated dodecahedron
| Truncated dodecahedron | |
|---|---|
 (Click here for rotating model) | |
| Type | Archimedean solid Uniform polyhedron |
| Elements | F = 32, E = 90, V = 60 (χ = 2) |
| Faces by sides | 20{3}+12{10} |
| Conway notation | tD |
| Schläfli symbols | t{5,3} |
| t0,1{5,3} | |
| Wythoff symbol | 2 3 | 5 |
| Coxeter diagram | |
| Symmetry group | Ih, H3, [5,3], (*532), order 120 |
| Rotation group | I, [5,3]+, (532), order 60 |
| Dihedral Angle | 10-10: 116.57° 3-10: 142.62° |
| References | U26, C29, W10 |
| Properties | Semiregular convex |
 Colored faces |
 3.10.10 (Vertex figure) |
 Triakis icosahedron (dual polyhedron) |
 Net |
In geometry, the truncated dodecahedron is an Archimedean solid. It has 12 regular decagonal faces, 20 regular triangular faces, 60 vertices and 90 edges.
Geometric relations
This polyhedron can be formed from a dodecahedron by truncating (cutting off) the corners so the pentagon faces become decagons and the corners become triangles.
It is used in the cell-transitive hyperbolic space-filling tessellation, the bitruncated icosahedral honeycomb.
Area and volume
The area A and the volume V of a truncated dodecahedron of edge length a are:
Cartesian coordinates
Cartesian coordinates for the vertices of a truncated dodecahedron with edge length 2φ − 2, centered at the origin,[1] are all even permutations of:
- (0, ±1/φ, ±(2 + φ))
- (±1/φ, ±φ, ±2φ)
- (±φ, ±2, ±(φ + 1))
where φ = 1 + √5/2 is the golden ratio.
Orthogonal projections
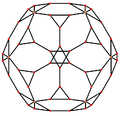
The truncated dodecahedron has five special orthogonal projections, centered, on a vertex, on two types of edges, and two types of faces: hexagonal and pentagonal. The last two correspond to the A2 and H2 Coxeter planes.
| Centered by | Vertex | Edge 3-10 |
Edge 10-10 |
Face Triangle |
Face Decagon |
|---|---|---|---|---|---|
| Image | 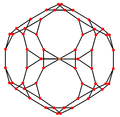 |
 |
 |
 |
 |
| Projective symmetry |
[2] | [2] | [2] | [6] | [10] |
| Dual image |
 |
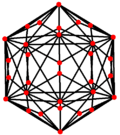 |
 |
 |
 |
Spherical tilings and Schlegel diagrams
The truncated dodecahedron can also be represented as a spherical tiling, and projected onto the plane via a stereographic projection. This projection is conformal, preserving angles but not areas or lengths. Straight lines on the sphere are projected as circular arcs on the plane.
Schlegel diagrams are similar, with a perspective projection and straight edges.
| Orthographic projection | Stereographic projections | |
|---|---|---|
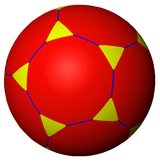 |
 Decagon-centered |
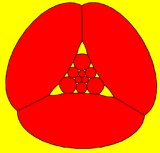 Triangle-centered |
 |
 |
 |
Vertex arrangement
It shares its vertex arrangement with three nonconvex uniform polyhedra:
 Truncated dodecahedron |
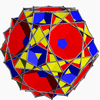 Great icosicosidodecahedron |
 Great ditrigonal dodecicosidodecahedron |
 Great dodecicosahedron |
Related polyhedra and tilings
It is part of a truncation process between a dodecahedron and icosahedron:
| Family of uniform icosahedral polyhedra | |||||||
|---|---|---|---|---|---|---|---|
| Symmetry: [5,3], (*532) | [5,3]+, (532) | ||||||
 |
 |
 |
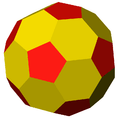 |
 |
 |
 |
 |
| {5,3} | t{5,3} | r{5,3} | t{3,5} | {3,5} | rr{5,3} | tr{5,3} | sr{5,3} |
| Duals to uniform polyhedra | |||||||
 |
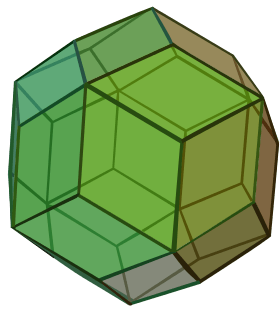 |
 |
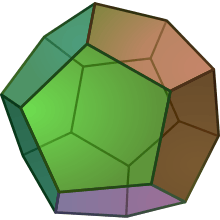 |
 |
 | ||
| V5.5.5 | V3.10.10 | V3.5.3.5 | V5.6.6 | V3.3.3.3.3 | V3.4.5.4 | V4.6.10 | V3.3.3.3.5 |
This polyhedron is topologically related as a part of sequence of uniform truncated polyhedra with vertex configurations (3.2n.2n), and [n,3] Coxeter group symmetry.
| *n32 symmetry mutation of truncated spherical tilings: t{n,3} | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry *n32 [n,3] |
Spherical | Euclid. | Compact hyperb. | Paraco. | |||||||
| *232 [2,3] |
*332 [3,3] |
*432 [4,3] |
*532 [5,3] |
*632 [6,3] |
*732 [7,3] |
*832 [8,3]... |
*∞32 [∞,3] | ||||
| Truncated figures |
|
 |
 |
 |
 |
 |
 |
 | |||
| Symbol | t{2,3} | t{3,3} | t{4,3} | t{5,3} | t{6,3} | t{7,3} | t{8,3} | t{∞,3} | |||
| Triakis figures |
 |
 |
 |
 |
 |
 | |||||
| Config. | V3.4.4 | V3.6.6 | V3.8.8 | V3.10.10 | V3.12.12 | V3.14.14 | V3.16.16 | V3.∞.∞ | |||
Truncated dodecahedral graph
| Truncated dodecahedral graph | |
|---|---|
|
5-fold symmetry schlegel diagram | |
| Vertices | 60 |
| Edges | 90 |
| Automorphisms | 120 |
| Chromatic number | 2 |
| Properties | Cubic, Hamiltonian, regular, zero-symmetric |
In the mathematical field of graph theory, a truncated dodecahedral graph is the graph of vertices and edges of the truncated dodecahedron, one of the Archimedean solids. It has 60 vertices and 90 edges, and is a cubic Archimedean graph.[2]
 Circular |
See also
- Spinning truncated cube
- Cube-connected cycles, a family of graphs that includes the skeleton of the truncated cube
Notes
- ↑ Weisstein, Eric W. "Icosahedral group". MathWorld.
- ↑ Read, R. C.; Wilson, R. J. (1998), An Atlas of Graphs, Oxford University Press, p. 269
References
- Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (Section 3-9)
- Cromwell, P. (1997). Polyhedra. United Kingdom: Cambridge. pp. 79–86 Archimedean solids. ISBN 0-521-55432-2.
External links
- Klitzing, Richard. "3D convex uniform polyhedra o3x5x - tid".
- Editable printable net of a truncated dodecahedron with interactive 3D view
- The Uniform Polyhedra
- Virtual Reality Polyhedra The Encyclopedia of Polyhedra