Octadecagon
| Regular octadecagon | |
|---|---|
 A regular octadecagon | |
| Type | Regular polygon |
| Edges and vertices | 18 |
| Schläfli symbol | {18}, t{9} |
| Coxeter diagram |
|
| Symmetry group | Dihedral (D18), order 2×18 |
| Internal angle (degrees) | 160° |
| Dual polygon | Self |
| Properties | Convex, cyclic, equilateral, isogonal, isotoxal |
An octadecagon (or octakaidecagon[1]) or 18-gon is an eighteen-sided polygon.[2]
Regular octadecagon
A regular octadecagon has a Schläfli symbol {18} and can be constructed as a quasiregular truncated enneagon, t{9}, which alternates two types of edges.
Construction
As 18 = 2 × 32, a regular octadecagon cannot be constructed using a compass and straightedge.[3] However, it is constructible using neusis, or an angle trisector. The following approximate construction is very similar to that of the enneagon, as an octadecagon can be constructed as a truncated enneagon. It is also feasible with exclusive use of compass and straightedge.

|
Symmetry
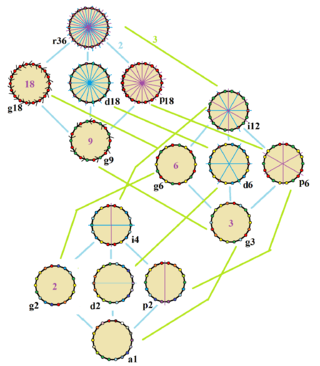
The regular octadecagon has Dih18 symmetry, order 36. There are 5 subgroup dihedral symmetries: Dih9, (Dih6, Dih3), and (Dih2 Dih1), and 6 cyclic group symmetries: (Z18, Z9), (Z6, Z3), and (Z2, Z1).
These 15 symmetries can be seen in 12 distinct symmetries on the octadecagon. John Conway labels these by a letter and group order.[4] Full symmetry of the regular form is r36 and no symmetry is labeled a1. The dihedral symmetries are divided depending on whether they pass through vertices (d for diagonal) or edges (p for perpendiculars), and i when reflection lines path through both edges and vertices. Cyclic symmetries in the middle column are labeled as g for their central gyration orders.
Each subgroup symmetry allows one or more degrees of freedom for irregular forms. Only the g18 subgroup has no degrees of freedom but can seen as directed edges.
Uses
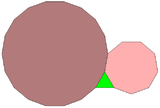
A regular triangle, nonagon, and octadecagon can completely surround a point in the plane, one of 17 different combinations of regular polygons with this property.[5] However, this pattern cannot be extended to an Archimedean tiling of the plane: because the triangle and the nonagon both have an odd number of sides, neither of them can be completely surrounded by a ring alternating the other two kinds of polygon.
The regular octadecagon can tessellate the plane with concave hexagonal gaps. And another tiling mixes in nonagons and octagonal gaps. The first tiling is related to a truncated hexagonal tiling, and the second the truncated trihexagonal tiling.
Related figures
An octadecagram is an 18-sided star polygon, represented by symbol {18/n}. There are two regular star polygons: {18/5} and {18/7}, using the same points, but connecting every fifth or seventh points. There are also five compounds: {18/2} is reduced to 2{9} or two enneagons, {18/3} is reduced to 3{6} or three hexagons, {18/4} and {18/8} are reduced to 2{9/2} and 2{9/4} or two enneagrams, {18/6} is reduced to 6{3} or 6 equilateral triangles, and finally {18/9} is reduced to 9{2} as nine digons.
| Compounds and star polygons | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Form | Convex polygon | Compounds | Star polygon | Compound | Star polygon | Compound | |||
| Image |  {18/1} = {18} |
.svg.png) {18/2} = 2{9} |
.svg.png) {18/3} = 3{6} |
.svg.png) {18/4} = 2{9/2} |
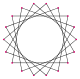 {18/5} |
.svg.png) {18/6} = 6{3} |
 {18/7} |
.svg.png) {18/8} = 2{9/4} |
.svg.png) {18/9} = 9{2} |
| Interior angle | 160° | 140° | 120° | 100° | 80° | 60° | 40° | 20° | 0° |
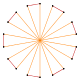
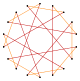
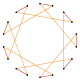
Deeper truncations of the regular enneagon and enneagrams can produce isogonal (vertex-transitive) intermediate octadecagram forms with equally spaced vertices and two edge lengths. Other truncations form double coverings: t{9/8}={18/8}=2{9/4}, t{9/4}={18/4}=2{9/2}, t{9/2}={18/2}=2{9}.[6]
| Vertex-transitive truncations of enneagon and enneagrams | |||||
|---|---|---|---|---|---|
| Quasiregular | isogonal | Quasiregular Double covering | |||
 t{9}={18} |
 |
 |
 |
 |
 t{9/8}={18/8} =2{9/4} |
 t{9/5}={18/5} |
 |
 |
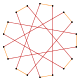 |
 |
 t{9/4}={18/4} =2{9/2} |
 t{9/7}={18/7} |
 |
 |
 |
 |
 t{9/2}={18/2} =2{9} |
Petrie polygons
The regular octadecagon is the Petrie polygon for a number of higher-dimensional polytopes, shown in these skew orthogonal projections from Coxeter planes:
| Octadecagonal petrie polygons | |||||||
|---|---|---|---|---|---|---|---|
| A17 | B9 | D10 | E7 | ||||
 17-simplex |
 9-orthoplex |
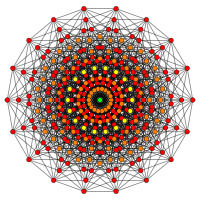 9-cube |
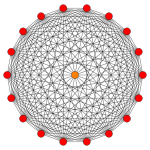 711 |
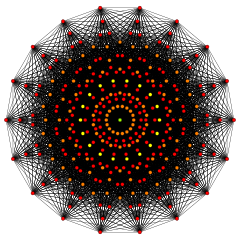 171 |
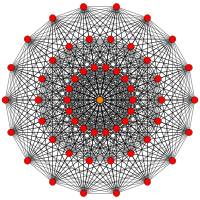 321 |
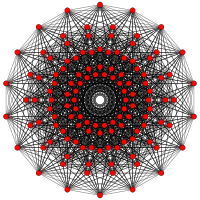 231 |
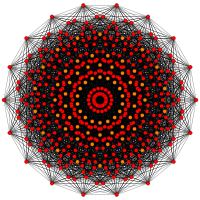 132 |
References
- ↑ Kinsey, L. Christine; Moore, Teresa E. (2002), Symmetry, Shape, and Surfaces: An Introduction to Mathematics Through Geometry, Springer, p. 86, ISBN 9781930190092.
- ↑ Adams, Henry (1907), Cassell's Engineer's Handbook: Comprising Facts and Formulæ, Principles and Practice, in All Branches of Engineering, D. McKay, p. 528.
- ↑ Conway, John B. (2010), Mathematical Connections: A Capstone Course, American Mathematical Society, p. 31, ISBN 9780821849798.
- ↑ John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, (2008) The Symmetries of Things, ISBN 978-1-56881-220-5 (Chapter 20, Generalized Schaefli symbols, Types of symmetry of a polygon pp. 275-278)
- ↑ Dallas, Elmslie William (1855), The Elements of Plane Practical Geometry, Etc, John W. Parker & Son, p. 134.
- ↑ The Lighter Side of Mathematics: Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and its History, (1994), Metamorphoses of polygons, Branko Grünbaum

