1 32 polytope
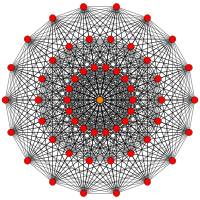 321 |
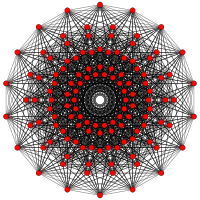 231 |
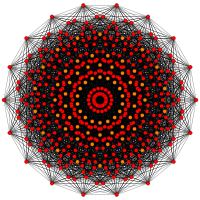 132 | |||
 Rectified 321 |
 birectified 321 | ||||
 Rectified 231 |
 Rectified 132 | ||||
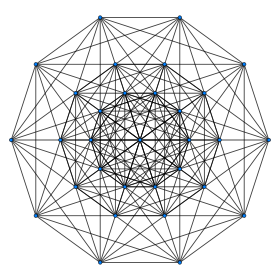
| Orthogonal projections in E7 Coxeter plane | |||||
|---|---|---|---|---|---|
In 7-dimensional geometry, 132 is a uniform polytope, constructed from the E7 group.
Its Coxeter symbol is 132, describing its bifurcating Coxeter-Dynkin diagram, with a single ring on the end of one of the 1-node sequences.
The rectified 132 is constructed by points at the mid-edges of the 132.
These polytopes are part of a family of 127 (27-1) convex uniform polytopes in 7-dimensions, made of uniform polytope facets and vertex figures, defined by all permutations of rings in this Coxeter-Dynkin diagram: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
1_32 polytope
| 132 | |
|---|---|
| Type | Uniform 7-polytope |
| Family | 1k2 polytope |
| Schläfli symbol | {3,33,2} |
| Coxeter symbol | 132 |
| Coxeter diagram | |
| 6-faces | 182: 56 122 126 131 |
| 5-faces | 4284: 756 121 1512 121 2016 {34} |
| 4-faces | 23688: 4032 {33} 7560 111 12096 {33} |
| Cells | 50400: 20160 {32} 30240 {32} |
| Faces | 40320 {3} |
| Edges | 10080 |
| Vertices | 576 |
| Vertex figure | t2{35} |
| Petrie polygon | Octadecagon |
| Coxeter group | E7, [33,2,1], order 2903040 |
| Properties | convex |
This polytope can tessellate 7-dimensional space, with symbol 133, and Coxeter-Dynkin diagram, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() . It is the Voronoi cell of the dual E7* lattice.[1]
. It is the Voronoi cell of the dual E7* lattice.[1]
Alternate names
- E. L. Elte named it V576 (for its 576 vertices) in his 1912 listing of semiregular polytopes.[2]
- Coxeter called it 132 for its bifurcating Coxeter-Dynkin diagram, with a single ring on the end of the 1-node branch.
- Pentacontihexa-hecatonicosihexa-exon (Acronym lin) - 56-126 facetted polyexon (Jonathan Bowers)[3]
Construction
It is created by a Wythoff construction upon a set of 7 hyperplane mirrors in 7-dimensional space.
The facet information can be extracted from its Coxeter-Dynkin diagram, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Removing the node on the end of the 2-length branch leaves the 6-demicube, 131, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Removing the node on the end of the 3-length branch leaves the 122, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
The vertex figure is determined by removing the ringed node and ringing the neighboring node. This makes the birectified 6-simplex, 032, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Images
| E7 | E6 / F4 | B7 / A6 |
|---|---|---|
 [18] |
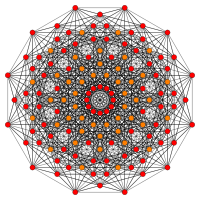 [12] |
 [7x2] |
| A5 | D7 / B6 | D6 / B5 |
 [6] |
 [12/2] |
 [10] |
| D5 / B4 / A4 | D4 / B3 / A2 / G2 | D3 / B2 / A3 |
 [8] |
 [6] |
 [4] |
Related polytopes and honeycombs
The 132 is third in a dimensional series of uniform polytopes and honeycombs, expressed by Coxeter as 13k series. The next figure is the Euclidean honeycomb 133 and the final is a noncompact hyperbolic honeycomb, 134.
| Space | Finite | Euclidean | Hyperbolic | |||
|---|---|---|---|---|---|---|
| n | 4 | 5 | 6 | 7 | 8 | 9 |
| Coxeter group |
A3A1 | A5 | D6 | E7 | =E7+ | =E7++ |
| Coxeter diagram |
||||||
| Symmetry | [3−1,3,1] | [30,3,1] | [31,3,1] | [32,3,1] | [[3<sup>3,3,1</sup>]] | [34,3,1] |
| Order | 48 | 720 | 23,040 | 2,903,040 | ∞ | |
| Graph |  |
 |
 |
- | - | |
| Name | 13,-1 | 130 | 131 | 132 | 133 | 134 |
| 1k2 figures in n dimensions | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Space | Finite | Euclidean | Hyperbolic | ||||||||
| n | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |||
| Coxeter group |
E3=A2A1 | E4=A4 | E5=D5 | E6 | E7 | E8 | E9 = = E8+ | E10 = = E8++ | |||
| Coxeter diagram |
|||||||||||
| Symmetry (order) |
[3−1,2,1] | [30,2,1] | [31,2,1] | [[3<sup>2,2,1</sup>]] | [33,2,1] | [34,2,1] | [35,2,1] | [36,2,1] | |||
| Order | 12 | 120 | 192 | 103,680 | 2,903,040 | 696,729,600 | ∞ | ||||
| Graph |  |
 |
 |
 |
 |
 |
- | - | |||
| Name | 1-1,2 | 102 | 112 | 122 | 132 | 142 | 152 | 162 | |||
Rectified 1_32 polytope
| Rectified 132 | |
|---|---|
| Type | Uniform 7-polytope |
| Schläfli symbol | t1{3,33,2} |
| Coxeter symbol | 0321 |
| Coxeter-Dynkin diagram | |
| 6-faces | 758 |
| 5-faces | 12348 |
| 4-faces | 72072 |
| Cells | 191520 |
| Faces | 241920 |
| Edges | 120960 |
| Vertices | 10080 |
| Vertex figure | {3,3}×{3}×{} |
| Coxeter group | E7, [33,2,1], order 2903040 |
| Properties | convex |
The rectified 132 (also called 0321) is a rectification of the 132 polytope, creating new vertices on the center of edge of the 132. Its vertex figure is a duoprism prism, the product of a regular tetrahedra and triangle, doubled into a prism: {3,3}×{3}×{}.
Alternate names
- Rectified pentacontihexa-hecatonicosihexa-exon for rectified 56-126 facetted polyexon (acronym rolin) (Jonathan Bowers)[4]
Construction
It is created by a Wythoff construction upon a set of 7 hyperplane mirrors in 7-dimensional space. These mirrors are represented by its Coxeter-Dynkin diagram, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() , and the ring represents the position of the active mirror(s).
, and the ring represents the position of the active mirror(s).
Removing the node on the end of the 3-length branch leaves the rectified 122 polytope, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Removing the node on the end of the 2-length branch leaves the demihexeract, 131, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Removing the node on the end of the 1-length branch leaves the birectified 6-simplex, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
The vertex figure is determined by removing the ringed node and ringing the neighboring node. This makes the tetrahedron-triangle duoprism prism, {3,3}×{3}×{}, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Images
| E7 | E6 / F4 | B7 / A6 |
|---|---|---|
 [18] |
 [12] |
 [14] |
| A5 | D7 / B6 | D6 / B5 |
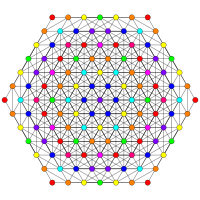 [6] |
 [12/2] |
 [10] |
| D5 / B4 / A4 | D4 / B3 / A2 / G2 | D3 / B2 / A3 |
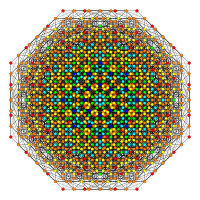 [8] |
 [6] |
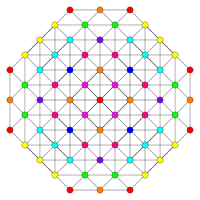 [4] |
See also
Notes
- ↑ The Voronoi Cells of the E6* and E7* Lattices, Edward Pervin
- ↑ Elte, 1912
- ↑ Klitzing, (o3o3o3x *c3o3o3o - lin)
- ↑ Klitzing, (o3o3x3o *c3o3o3o - rolin)
References
- Elte, E. L. (1912), The Semiregular Polytopes of the Hyperspaces, Groningen: University of Groningen
- H. S. M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- Klitzing, Richard. "7D uniform polytopes (polyexa)". o3o3o3x *c3o3o3o - lin, o3o3x3o *c3o3o3o - rolin
| Fundamental convex regular and uniform polytopes in dimensions 2–10 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Family | An | Bn | I2(p) / Dn | E6 / E7 / E8 / E9 / E10 / F4 / G2 | Hn | |||||||
| Regular polygon | Triangle | Square | p-gon | Hexagon | Pentagon | |||||||
| Uniform polyhedron | Tetrahedron | Octahedron • Cube | Demicube | Dodecahedron • Icosahedron | ||||||||
| Uniform 4-polytope | 5-cell | 16-cell • Tesseract | Demitesseract | 24-cell | 120-cell • 600-cell | |||||||
| Uniform 5-polytope | 5-simplex | 5-orthoplex • 5-cube | 5-demicube | |||||||||
| Uniform 6-polytope | 6-simplex | 6-orthoplex • 6-cube | 6-demicube | 122 • 221 | ||||||||
| Uniform 7-polytope | 7-simplex | 7-orthoplex • 7-cube | 7-demicube | 132 • 231 • 321 | ||||||||
| Uniform 8-polytope | 8-simplex | 8-orthoplex • 8-cube | 8-demicube | 142 • 241 • 421 | ||||||||
| Uniform 9-polytope | 9-simplex | 9-orthoplex • 9-cube | 9-demicube | |||||||||
| Uniform 10-polytope | 10-simplex | 10-orthoplex • 10-cube | 10-demicube | |||||||||
| Uniform n-polytope | n-simplex | n-orthoplex • n-cube | n-demicube | 1k2 • 2k1 • k21 | n-pentagonal polytope | |||||||
| Topics: Polytope families • Regular polytope • List of regular polytopes and compounds | ||||||||||||