Uniform 7-polytope
In seven-dimensional geometry, a 7-polytope is a polytope contained by 6-polytope facets. Each 5-polytope ridge being shared by exactly two 6-polytope facets.
A uniform 7-polytope is one which is vertex-transitive, and constructed from uniform 6-polytope facets.
Regular 7-polytopes
Regular 7-polytopes are represented by the Schläfli symbol {p,q,r,s,t,u} with u {p,q,r,s,t} 6-polytopes facets around each 4-face.
There are exactly three such convex regular 7-polytopes:
- {3,3,3,3,3,3} - 7-simplex
- {4,3,3,3,3,3} - 7-cube
- {3,3,3,3,3,4} - 7-orthoplex
There are no nonconvex regular 7-polytopes.
Characteristics
The topology of any given 7-polytope is defined by its Betti numbers and torsion coefficients.[1]
The value of the Euler characteristic used to characterise polyhedra does not generalize usefully to higher dimensions, whatever their underlying topology. This inadequacy of the Euler characteristic to reliably distinguish between different topologies in higher dimensions led to the discovery of the more sophisticated Betti numbers.[1]
Similarly, the notion of orientability of a polyhedron is insufficient to characterise the surface twistings of toroidal polytopes, and this led to the use of torsion coefficients.[1]
Uniform 7-polytopes by fundamental Coxeter groups
Uniform 7-polytopes with reflective symmetry can be generated by these four Coxeter groups, represented by permutations of rings of the Coxeter-Dynkin diagrams:
| # | Coxeter group | Regular and semiregular forms | Uniform count | ||
|---|---|---|---|---|---|
| 1 | A7 | [36] |
|
71 | |
| 2 | B7 | [4,35] |
|
127 + 32 | |
| 3 | D7 | [33,1,1] |
|
95 (0 unique) | |
| 4 | E7 | [33,2,1] | 127 | ||
| Prismatic finite Coxeter groups | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| # | Coxeter group | Coxeter diagram | |||||||||
| 6+1 | |||||||||||
| 1 | A6A1 | [35]×[ ] | | ||||||||
| 2 | BC6A1 | [4,34]×[ ] | | ||||||||
| 3 | D6A1 | [33,1,1]×[ ] | | ||||||||
| 4 | E6A1 | [32,2,1]×[ ] | | ||||||||
| 5+2 | |||||||||||
| 1 | A5I2(p) | [3,3,3]×[p] | | ||||||||
| 2 | BC5I2(p) | [4,3,3]×[p] | | ||||||||
| 3 | D5I2(p) | [32,1,1]×[p] | | ||||||||
| 5+1+1 | |||||||||||
| 1 | A5A12 | [3,3,3]×[ ]2 | | ||||||||
| 2 | BC5A12 | [4,3,3]×[ ]2 | | ||||||||
| 3 | D5A12 | [32,1,1]×[ ]2 | | ||||||||
| 4+3 | |||||||||||
| 1 | A4A3 | [3,3,3]×[3,3] | | ||||||||
| 2 | A4B3 | [3,3,3]×[4,3] | | ||||||||
| 3 | A4H3 | [3,3,3]×[5,3] | | ||||||||
| 4 | BC4A3 | [4,3,3]×[3,3] | | ||||||||
| 5 | BC4B3 | [4,3,3]×[4,3] | | ||||||||
| 6 | BC4H3 | [4,3,3]×[5,3] | | ||||||||
| 7 | H4A3 | [5,3,3]×[3,3] | | ||||||||
| 8 | H4B3 | [5,3,3]×[4,3] | | ||||||||
| 9 | H4H3 | [5,3,3]×[5,3] | | ||||||||
| 10 | F4A3 | [3,4,3]×[3,3] | | ||||||||
| 11 | F4B3 | [3,4,3]×[4,3] | | ||||||||
| 12 | F4H3 | [3,4,3]×[5,3] | | ||||||||
| 13 | D4A3 | [31,1,1]×[3,3] | | ||||||||
| 14 | D4B3 | [31,1,1]×[4,3] | | ||||||||
| 15 | D4H3 | [31,1,1]×[5,3] | | ||||||||
| 4+2+1 | |||||||||||
| 1 | A4I2(p)A1 | [3,3,3]×[p]×[ ] | | ||||||||
| 2 | BC4I2(p)A1 | [4,3,3]×[p]×[ ] | | ||||||||
| 3 | F4I2(p)A1 | [3,4,3]×[p]×[ ] | | ||||||||
| 4 | H4I2(p)A1 | [5,3,3]×[p]×[ ] | | ||||||||
| 5 | D4I2(p)A1 | [31,1,1]×[p]×[ ] | | ||||||||
| 4+1+1+1 | |||||||||||
| 1 | A4A13 | [3,3,3]×[ ]3 | | ||||||||
| 2 | BC4A13 | [4,3,3]×[ ]3 | | ||||||||
| 3 | F4A13 | [3,4,3]×[ ]3 | | ||||||||
| 4 | H4A13 | [5,3,3]×[ ]3 | | ||||||||
| 5 | D4A13 | [31,1,1]×[ ]3 | | ||||||||
| 3+3+1 | |||||||||||
| 1 | A3A3A1 | [3,3]×[3,3]×[ ] | | ||||||||
| 2 | A3B3A1 | [3,3]×[4,3]×[ ] | | ||||||||
| 3 | A3H3A1 | [3,3]×[5,3]×[ ] | | ||||||||
| 4 | BC3B3A1 | [4,3]×[4,3]×[ ] | | ||||||||
| 5 | BC3H3A1 | [4,3]×[5,3]×[ ] | | ||||||||
| 6 | H3A3A1 | [5,3]×[5,3]×[ ] | | ||||||||
| 3+2+2 | |||||||||||
| 1 | A3I2(p)I2(q) | [3,3]×[p]×[q] | | ||||||||
| 2 | BC3I2(p)I2(q) | [4,3]×[p]×[q] | | ||||||||
| 3 | H3I2(p)I2(q) | [5,3]×[p]×[q] | | ||||||||
| 3+2+1+1 | |||||||||||
| 1 | A3I2(p)A12 | [3,3]×[p]×[ ]2 | | ||||||||
| 2 | BC3I2(p)A12 | [4,3]×[p]×[ ]2 | | ||||||||
| 3 | H3I2(p)A12 | [5,3]×[p]×[ ]2 | | ||||||||
| 3+1+1+1+1 | |||||||||||
| 1 | A3A14 | [3,3]×[ ]4 | | ||||||||
| 2 | BC3A14 | [4,3]×[ ]4 | | ||||||||
| 3 | H3A14 | [5,3]×[ ]4 | | ||||||||
| 2+2+2+1 | |||||||||||
| 1 | I2(p)I2(q)I2(r)A1 | [p]×[q]×[r]×[ ] | | ||||||||
| 2+2+1+1+1 | |||||||||||
| 1 | I2(p)I2(q)A13 | [p]×[q]×[ ]3 | | ||||||||
| 2+1+1+1+1+1 | |||||||||||
| 1 | I2(p)A15 | [p]×[ ]5 | | ||||||||
| 1+1+1+1+1+1+1 | |||||||||||
| 1 | A17 | [ ]7 | | ||||||||
The A7 family
The A7 family has symmetry of order 40320 (8 factorial).
There are 71 (64+8-1) forms based on all permutations of the Coxeter-Dynkin diagrams with one or more rings. All 71 are enumerated below. Norman Johnson's truncation names are given. Bowers names and acronym are also given for cross-referencing.
See also a list of A7 polytopes for symmetric Coxeter plane graphs of these polytopes.
| A7 uniform polytopes | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| # | Coxeter-Dynkin diagram | Truncation indices |
Johnson name Bowers name (and acronym) |
Basepoint | Element counts | ||||||
| 6 | 5 | 4 | 3 | 2 | 1 | 0 | |||||
| 1 | t0 | 7-simplex (oca) | (0,0,0,0,0,0,0,1) | 8 | 28 | 56 | 70 | 56 | 28 | 8 | |
| 2 | t1 | Rectified 7-simplex (roc) | (0,0,0,0,0,0,1,1) | 16 | 84 | 224 | 350 | 336 | 168 | 28 | |
| 3 | t2 | Birectified 7-simplex (broc) | (0,0,0,0,0,1,1,1) | 16 | 112 | 392 | 770 | 840 | 420 | 56 | |
| 4 | t3 | Trirectified 7-simplex (he) | (0,0,0,0,1,1,1,1) | 16 | 112 | 448 | 980 | 1120 | 560 | 70 | |
| 5 | t0,1 | Truncated 7-simplex (toc) | (0,0,0,0,0,0,1,2) | 16 | 84 | 224 | 350 | 336 | 196 | 56 | |
| 6 | t0,2 | Cantellated 7-simplex (saro) | (0,0,0,0,0,1,1,2) | 44 | 308 | 980 | 1750 | 1876 | 1008 | 168 | |
| 7 | t1,2 | Bitruncated 7-simplex (bittoc) | (0,0,0,0,0,1,2,2) | 588 | 168 | ||||||
| 8 | t0,3 | Runcinated 7-simplex (spo) | (0,0,0,0,1,1,1,2) | 100 | 756 | 2548 | 4830 | 4760 | 2100 | 280 | |
| 9 | t1,3 | Bicantellated 7-simplex (sabro) | (0,0,0,0,1,1,2,2) | 2520 | 420 | ||||||
| 10 | t2,3 | Tritruncated 7-simplex (tattoc) | (0,0,0,0,1,2,2,2) | 980 | 280 | ||||||
| 11 | t0,4 | Stericated 7-simplex (sco) | (0,0,0,1,1,1,1,2) | 2240 | 280 | ||||||
| 12 | t1,4 | Biruncinated 7-simplex (sibpo) | (0,0,0,1,1,1,2,2) | 4200 | 560 | ||||||
| 13 | t2,4 | Tricantellated 7-simplex (stiroh) | (0,0,0,1,1,2,2,2) | 3360 | 560 | ||||||
| 14 | t0,5 | Pentellated 7-simplex (seto) | (0,0,1,1,1,1,1,2) | 1260 | 168 | ||||||
| 15 | t1,5 | Bistericated 7-simplex (sabach) | (0,0,1,1,1,1,2,2) | 3360 | 420 | ||||||
| 16 | t0,6 | Hexicated 7-simplex (suph) | (0,1,1,1,1,1,1,2) | 336 | 56 | ||||||
| 17 | t0,1,2 | Cantitruncated 7-simplex (garo) | (0,0,0,0,0,1,2,3) | 1176 | 336 | ||||||
| 18 | t0,1,3 | Runcitruncated 7-simplex (patto) | (0,0,0,0,1,1,2,3) | 4620 | 840 | ||||||
| 19 | t0,2,3 | Runcicantellated 7-simplex (paro) | (0,0,0,0,1,2,2,3) | 3360 | 840 | ||||||
| 20 | t1,2,3 | Bicantitruncated 7-simplex (gabro) | (0,0,0,0,1,2,3,3) | 2940 | 840 | ||||||
| 21 | t0,1,4 | Steritruncated 7-simplex (cato) | (0,0,0,1,1,1,2,3) | 7280 | 1120 | ||||||
| 22 | t0,2,4 | Stericantellated 7-simplex (caro) | (0,0,0,1,1,2,2,3) | 10080 | 1680 | ||||||
| 23 | t1,2,4 | Biruncitruncated 7-simplex (bipto) | (0,0,0,1,1,2,3,3) | 8400 | 1680 | ||||||
| 24 | t0,3,4 | Steriruncinated 7-simplex (cepo) | (0,0,0,1,2,2,2,3) | 5040 | 1120 | ||||||
| 25 | t1,3,4 | Biruncicantellated 7-simplex (bipro) | (0,0,0,1,2,2,3,3) | 7560 | 1680 | ||||||
| 26 | t2,3,4 | Tricantitruncated 7-simplex (gatroh) | (0,0,0,1,2,3,3,3) | 3920 | 1120 | ||||||
| 27 | t0,1,5 | Pentitruncated 7-simplex (teto) | (0,0,1,1,1,1,2,3) | 5460 | 840 | ||||||
| 28 | t0,2,5 | Penticantellated 7-simplex (tero) | (0,0,1,1,1,2,2,3) | 11760 | 1680 | ||||||
| 29 | t1,2,5 | Bisteritruncated 7-simplex (bacto) | (0,0,1,1,1,2,3,3) | 9240 | 1680 | ||||||
| 30 | t0,3,5 | Pentiruncinated 7-simplex (tepo) | (0,0,1,1,2,2,2,3) | 10920 | 1680 | ||||||
| 31 | t1,3,5 | Bistericantellated 7-simplex (bacroh) | (0,0,1,1,2,2,3,3) | 15120 | 2520 | ||||||
| 32 | t0,4,5 | Pentistericated 7-simplex (teco) | (0,0,1,2,2,2,2,3) | 4200 | 840 | ||||||
| 33 | t0,1,6 | Hexitruncated 7-simplex (puto) | (0,1,1,1,1,1,2,3) | 1848 | 336 | ||||||
| 34 | t0,2,6 | Hexicantellated 7-simplex (puro) | (0,1,1,1,1,2,2,3) | 5880 | 840 | ||||||
| 35 | t0,3,6 | Hexiruncinated 7-simplex (puph) | (0,1,1,1,2,2,2,3) | 8400 | 1120 | ||||||
| 36 | t0,1,2,3 | Runcicantitruncated 7-simplex (gapo) | (0,0,0,0,1,2,3,4) | 5880 | 1680 | ||||||
| 37 | t0,1,2,4 | Stericantitruncated 7-simplex (cagro) | (0,0,0,1,1,2,3,4) | 16800 | 3360 | ||||||
| 38 | t0,1,3,4 | Steriruncitruncated 7-simplex (capto) | (0,0,0,1,2,2,3,4) | 13440 | 3360 | ||||||
| 39 | t0,2,3,4 | Steriruncicantellated 7-simplex (capro) | (0,0,0,1,2,3,3,4) | 13440 | 3360 | ||||||
| 40 | t1,2,3,4 | Biruncicantitruncated 7-simplex (gibpo) | (0,0,0,1,2,3,4,4) | 11760 | 3360 | ||||||
| 41 | t0,1,2,5 | Penticantitruncated 7-simplex (tegro) | (0,0,1,1,1,2,3,4) | 18480 | 3360 | ||||||
| 42 | t0,1,3,5 | Pentiruncitruncated 7-simplex (tapto) | (0,0,1,1,2,2,3,4) | 27720 | 5040 | ||||||
| 43 | t0,2,3,5 | Pentiruncicantellated 7-simplex (tapro) | (0,0,1,1,2,3,3,4) | 25200 | 5040 | ||||||
| 44 | t1,2,3,5 | Bistericantitruncated 7-simplex (bacogro) | (0,0,1,1,2,3,4,4) | 22680 | 5040 | ||||||
| 45 | t0,1,4,5 | Pentisteritruncated 7-simplex (tecto) | (0,0,1,2,2,2,3,4) | 15120 | 3360 | ||||||
| 46 | t0,2,4,5 | Pentistericantellated 7-simplex (tecro) | (0,0,1,2,2,3,3,4) | 25200 | 5040 | ||||||
| 47 | t1,2,4,5 | Bisteriruncitruncated 7-simplex (bicpath) | (0,0,1,2,2,3,4,4) | 20160 | 5040 | ||||||
| 48 | t0,3,4,5 | Pentisteriruncinated 7-simplex (tacpo) | (0,0,1,2,3,3,3,4) | 15120 | 3360 | ||||||
| 49 | t0,1,2,6 | Hexicantitruncated 7-simplex (pugro) | (0,1,1,1,1,2,3,4) | 8400 | 1680 | ||||||
| 50 | t0,1,3,6 | Hexiruncitruncated 7-simplex (pugato) | (0,1,1,1,2,2,3,4) | 20160 | 3360 | ||||||
| 51 | t0,2,3,6 | Hexiruncicantellated 7-simplex (pugro) | (0,1,1,1,2,3,3,4) | 16800 | 3360 | ||||||
| 52 | t0,1,4,6 | Hexisteritruncated 7-simplex (pucto) | (0,1,1,2,2,2,3,4) | 20160 | 3360 | ||||||
| 53 | t0,2,4,6 | Hexistericantellated 7-simplex (pucroh) | (0,1,1,2,2,3,3,4) | 30240 | 5040 | ||||||
| 54 | t0,1,5,6 | Hexipentitruncated 7-simplex (putath) | (0,1,2,2,2,2,3,4) | 8400 | 1680 | ||||||
| 55 | t0,1,2,3,4 | Steriruncicantitruncated 7-simplex (gecco) | (0,0,0,1,2,3,4,5) | 23520 | 6720 | ||||||
| 56 | t0,1,2,3,5 | Pentiruncicantitruncated 7-simplex (tegapo) | (0,0,1,1,2,3,4,5) | 45360 | 10080 | ||||||
| 57 | t0,1,2,4,5 | Pentistericantitruncated 7-simplex (tecagro) | (0,0,1,2,2,3,4,5) | 40320 | 10080 | ||||||
| 58 | t0,1,3,4,5 | Pentisteriruncitruncated 7-simplex (tacpeto) | (0,0,1,2,3,3,4,5) | 40320 | 10080 | ||||||
| 59 | t0,2,3,4,5 | Pentisteriruncicantellated 7-simplex (tacpro) | (0,0,1,2,3,4,4,5) | 40320 | 10080 | ||||||
| 60 | t1,2,3,4,5 | Bisteriruncicantitruncated 7-simplex (gabach) | (0,0,1,2,3,4,5,5) | 35280 | 10080 | ||||||
| 61 | t0,1,2,3,6 | Hexiruncicantitruncated 7-simplex (pugopo) | (0,1,1,1,2,3,4,5) | 30240 | 6720 | ||||||
| 62 | t0,1,2,4,6 | Hexistericantitruncated 7-simplex (pucagro) | (0,1,1,2,2,3,4,5) | 50400 | 10080 | ||||||
| 63 | t0,1,3,4,6 | Hexisteriruncitruncated 7-simplex (pucpato) | (0,1,1,2,3,3,4,5) | 45360 | 10080 | ||||||
| 64 | t0,2,3,4,6 | Hexisteriruncicantellated 7-simplex (pucproh) | (0,1,1,2,3,4,4,5) | 45360 | 10080 | ||||||
| 65 | t0,1,2,5,6 | Hexipenticantitruncated 7-simplex (putagro) | (0,1,2,2,2,3,4,5) | 30240 | 6720 | ||||||
| 66 | t0,1,3,5,6 | Hexipentiruncitruncated 7-simplex (putpath) | (0,1,2,2,3,3,4,5) | 50400 | 10080 | ||||||
| 67 | t0,1,2,3,4,5 | Pentisteriruncicantitruncated 7-simplex (geto) | (0,0,1,2,3,4,5,6) | 70560 | 20160 | ||||||
| 68 | t0,1,2,3,4,6 | Hexisteriruncicantitruncated 7-simplex (pugaco) | (0,1,1,2,3,4,5,6) | 80640 | 20160 | ||||||
| 69 | t0,1,2,3,5,6 | Hexipentiruncicantitruncated 7-simplex (putgapo) | (0,1,2,2,3,4,5,6) | 80640 | 20160 | ||||||
| 70 | t0,1,2,4,5,6 | Hexipentistericantitruncated 7-simplex (putcagroh) | (0,1,2,3,3,4,5,6) | 80640 | 20160 | ||||||
| 71 | t0,1,2,3,4,5,6 | Omnitruncated 7-simplex (guph) | (0,1,2,3,4,5,6,7) | 141120 | 40320 | ||||||
The B7 family
The B7 family has symmetry of order 645120 (7 factorial x 27).
There are 127 forms based on all permutations of the Coxeter-Dynkin diagrams with one or more rings. Johnson and Bowers names.
See also a list of B7 polytopes for symmetric Coxeter plane graphs of these polytopes.
| B7 uniform polytopes | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| # | Coxeter-Dynkin diagram t-notation |
Name (BSA) | Base point | Element counts | |||||||
| 6 | 5 | 4 | 3 | 2 | 1 | 0 | |||||
| 1 | t0{3,3,3,3,3,4} | 7-orthoplex (zee) | (0,0,0,0,0,0,1)√2 | 128 | 448 | 672 | 560 | 280 | 84 | 14 | |
| 2 | t1{3,3,3,3,3,4} | Rectified 7-orthoplex (rez) | (0,0,0,0,0,1,1)√2 | 142 | 1344 | 3360 | 3920 | 2520 | 840 | 84 | |
| 3 | t2{3,3,3,3,3,4} | Birectified 7-orthoplex (barz) | (0,0,0,0,1,1,1)√2 | 142 | 1428 | 6048 | 10640 | 8960 | 3360 | 280 | |
| 4 | t3{4,3,3,3,3,3} | Trirectified 7-cube (sez) | (0,0,0,1,1,1,1)√2 | 142 | 1428 | 6328 | 14560 | 15680 | 6720 | 560 | |
| 5 | t2{4,3,3,3,3,3} | Birectified 7-cube (bersa) | (0,0,1,1,1,1,1)√2 | 142 | 1428 | 5656 | 11760 | 13440 | 6720 | 672 | |
| 6 | t1{4,3,3,3,3,3} | Rectified 7-cube (rasa) | (0,1,1,1,1,1,1)√2 | 142 | 980 | 2968 | 5040 | 5152 | 2688 | 448 | |
| 7 | t0{4,3,3,3,3,3} | 7-cube (hept) | (0,0,0,0,0,0,0)√2 + (1,1,1,1,1,1,1) | 14 | 84 | 280 | 560 | 672 | 448 | 128 | |
| 8 | t0,1{3,3,3,3,3,4} | Truncated 7-orthoplex (Taz) | (0,0,0,0,0,1,2)√2 | 142 | 1344 | 3360 | 4760 | 2520 | 924 | 168 | |
| 9 | t0,2{3,3,3,3,3,4} | Cantellated 7-orthoplex (Sarz) | (0,0,0,0,1,1,2)√2 | 226 | 4200 | 15456 | 24080 | 19320 | 7560 | 840 | |
| 10 | t1,2{3,3,3,3,3,4} | Bitruncated 7-orthoplex (Botaz) | (0,0,0,0,1,2,2)√2 | 4200 | 840 | ||||||
| 11 | t0,3{3,3,3,3,3,4} | Runcinated 7-orthoplex (Spaz) | (0,0,0,1,1,1,2)√2 | 23520 | 2240 | ||||||
| 12 | t1,3{3,3,3,3,3,4} | Bicantellated 7-orthoplex (Sebraz) | (0,0,0,1,1,2,2)√2 | 26880 | 3360 | ||||||
| 13 | t2,3{3,3,3,3,3,4} | Tritruncated 7-orthoplex (Totaz) | (0,0,0,1,2,2,2)√2 | 10080 | 2240 | ||||||
| 14 | t0,4{3,3,3,3,3,4} | Stericated 7-orthoplex (Scaz) | (0,0,1,1,1,1,2)√2 | 33600 | 3360 | ||||||
| 15 | t1,4{3,3,3,3,3,4} | Biruncinated 7-orthoplex (Sibpaz) | (0,0,1,1,1,2,2)√2 | 60480 | 6720 | ||||||
| 16 | t2,4{4,3,3,3,3,3} | Tricantellated 7-cube (Strasaz) | (0,0,1,1,2,2,2)√2 | 47040 | 6720 | ||||||
| 17 | t2,3{4,3,3,3,3,3} | Tritruncated 7-cube (Tatsa) | (0,0,1,2,2,2,2)√2 | 13440 | 3360 | ||||||
| 18 | t0,5{3,3,3,3,3,4} | Pentellated 7-orthoplex (Staz) | (0,1,1,1,1,1,2)√2 | 20160 | 2688 | ||||||
| 19 | t1,5{4,3,3,3,3,3} | Bistericated 7-cube (Sabcosaz) | (0,1,1,1,1,2,2)√2 | 53760 | 6720 | ||||||
| 20 | t1,4{4,3,3,3,3,3} | Biruncinated 7-cube (Sibposa) | (0,1,1,1,2,2,2)√2 | 67200 | 8960 | ||||||
| 21 | t1,3{4,3,3,3,3,3} | Bicantellated 7-cube (Sibrosa) | (0,1,1,2,2,2,2)√2 | 40320 | 6720 | ||||||
| 22 | t1,2{4,3,3,3,3,3} | Bitruncated 7-cube (Betsa) | (0,1,2,2,2,2,2)√2 | 9408 | 2688 | ||||||
| 23 | t0,6{4,3,3,3,3,3} | Hexicated 7-cube (Supposaz) | (0,0,0,0,0,0,1)√2 + (1,1,1,1,1,1,1) | 5376 | 896 | ||||||
| 24 | t0,5{4,3,3,3,3,3} | Pentellated 7-cube (Stesa) | (0,0,0,0,0,1,1)√2 + (1,1,1,1,1,1,1) | 20160 | 2688 | ||||||
| 25 | t0,4{4,3,3,3,3,3} | Stericated 7-cube (Scosa) | (0,0,0,0,1,1,1)√2 + (1,1,1,1,1,1,1) | 35840 | 4480 | ||||||
| 26 | t0,3{4,3,3,3,3,3} | Runcinated 7-cube (Spesa) | (0,0,0,1,1,1,1)√2 + (1,1,1,1,1,1,1) | 33600 | 4480 | ||||||
| 27 | t0,2{4,3,3,3,3,3} | Cantellated 7-cube (Sersa) | (0,0,1,1,1,1,1)√2 + (1,1,1,1,1,1,1) | 16128 | 2688 | ||||||
| 28 | t0,1{4,3,3,3,3,3} | Truncated 7-cube (Tasa) | (0,1,1,1,1,1,1)√2 + (1,1,1,1,1,1,1) | 142 | 980 | 2968 | 5040 | 5152 | 3136 | 896 | |
| 29 | t0,1,2{3,3,3,3,3,4} | Cantitruncated 7-orthoplex (Garz) | (0,1,2,3,3,3,3)√2 | 8400 | 1680 | ||||||
| 30 | t0,1,3{3,3,3,3,3,4} | Runcitruncated 7-orthoplex (Potaz) | (0,1,2,2,3,3,3)√2 | 50400 | 6720 | ||||||
| 31 | t0,2,3{3,3,3,3,3,4} | Runcicantellated 7-orthoplex (Parz) | (0,1,1,2,3,3,3)√2 | 33600 | 6720 | ||||||
| 32 | t1,2,3{3,3,3,3,3,4} | Bicantitruncated 7-orthoplex (Gebraz) | (0,0,1,2,3,3,3)√2 | 30240 | 6720 | ||||||
| 33 | t0,1,4{3,3,3,3,3,4} | Steritruncated 7-orthoplex (Catz) | (0,0,1,1,1,2,3)√2 | 107520 | 13440 | ||||||
| 34 | t0,2,4{3,3,3,3,3,4} | Stericantellated 7-orthoplex (Craze) | (0,0,1,1,2,2,3)√2 | 141120 | 20160 | ||||||
| 35 | t1,2,4{3,3,3,3,3,4} | Biruncitruncated 7-orthoplex (Baptize) | (0,0,1,1,2,3,3)√2 | 120960 | 20160 | ||||||
| 36 | t0,3,4{3,3,3,3,3,4} | Steriruncinated 7-orthoplex (Copaz) | (0,1,1,1,2,3,3)√2 | 67200 | 13440 | ||||||
| 37 | t1,3,4{3,3,3,3,3,4} | Biruncicantellated 7-orthoplex (Boparz) | (0,0,1,2,2,3,3)√2 | 100800 | 20160 | ||||||
| 38 | t2,3,4{4,3,3,3,3,3} | Tricantitruncated 7-cube (Gotrasaz) | (0,0,0,1,2,3,3)√2 | 53760 | 13440 | ||||||
| 39 | t0,1,5{3,3,3,3,3,4} | Pentitruncated 7-orthoplex (Tetaz) | (0,1,1,1,1,2,3)√2 | 87360 | 13440 | ||||||
| 40 | t0,2,5{3,3,3,3,3,4} | Penticantellated 7-orthoplex (Teroz) | (0,1,1,1,2,2,3)√2 | 188160 | 26880 | ||||||
| 41 | t1,2,5{3,3,3,3,3,4} | Bisteritruncated 7-orthoplex (Boctaz) | (0,1,1,1,2,3,3)√2 | 147840 | 26880 | ||||||
| 42 | t0,3,5{3,3,3,3,3,4} | Pentiruncinated 7-orthoplex (Topaz) | (0,1,1,2,2,2,3)√2 | 174720 | 26880 | ||||||
| 43 | t1,3,5{4,3,3,3,3,3} | Bistericantellated 7-cube (Bacresaz) | (0,1,1,2,2,3,3)√2 | 241920 | 40320 | ||||||
| 44 | t1,3,4{4,3,3,3,3,3} | Biruncicantellated 7-cube (Bopresa) | (0,1,1,2,3,3,3)√2 | 120960 | 26880 | ||||||
| 45 | t0,4,5{3,3,3,3,3,4} | Pentistericated 7-orthoplex (Tocaz) | (0,1,2,2,2,2,3)√2 | 67200 | 13440 | ||||||
| 46 | t1,2,5{4,3,3,3,3,3} | Bisteritruncated 7-cube (Bactasa) | (0,1,2,2,2,3,3)√2 | 147840 | 26880 | ||||||
| 47 | t1,2,4{4,3,3,3,3,3} | Biruncitruncated 7-cube (Biptesa) | (0,1,2,2,3,3,3)√2 | 134400 | 26880 | ||||||
| 48 | t1,2,3{4,3,3,3,3,3} | Bicantitruncated 7-cube (Gibrosa) | (0,1,2,3,3,3,3)√2 | 47040 | 13440 | ||||||
| 49 | t0,1,6{3,3,3,3,3,4} | Hexitruncated 7-orthoplex (Putaz) | (0,0,0,0,0,1,2)√2 + (1,1,1,1,1,1,1) | 29568 | 5376 | ||||||
| 50 | t0,2,6{3,3,3,3,3,4} | Hexicantellated 7-orthoplex (Puraz) | (0,0,0,0,1,1,2)√2 + (1,1,1,1,1,1,1) | 94080 | 13440 | ||||||
| 51 | t0,4,5{4,3,3,3,3,3} | Pentistericated 7-cube (Tacosa) | (0,0,0,0,1,2,2)√2 + (1,1,1,1,1,1,1) | 67200 | 13440 | ||||||
| 52 | t0,3,6{4,3,3,3,3,3} | Hexiruncinated 7-cube (Pupsez) | (0,0,0,1,1,1,2)√2 + (1,1,1,1,1,1,1) | 134400 | 17920 | ||||||
| 53 | t0,3,5{4,3,3,3,3,3} | Pentiruncinated 7-cube (Tapsa) | (0,0,0,1,1,2,2)√2 + (1,1,1,1,1,1,1) | 174720 | 26880 | ||||||
| 54 | t0,3,4{4,3,3,3,3,3} | Steriruncinated 7-cube (Capsa) | (0,0,0,1,2,2,2)√2 + (1,1,1,1,1,1,1) | 80640 | 17920 | ||||||
| 55 | t0,2,6{4,3,3,3,3,3} | Hexicantellated 7-cube (Purosa) | (0,0,1,1,1,1,2)√2 + (1,1,1,1,1,1,1) | 94080 | 13440 | ||||||
| 56 | t0,2,5{4,3,3,3,3,3} | Penticantellated 7-cube (Tersa) | (0,0,1,1,1,2,2)√2 + (1,1,1,1,1,1,1) | 188160 | 26880 | ||||||
| 57 | t0,2,4{4,3,3,3,3,3} | Stericantellated 7-cube (Carsa) | (0,0,1,1,2,2,2)√2 + (1,1,1,1,1,1,1) | 161280 | 26880 | ||||||
| 58 | t0,2,3{4,3,3,3,3,3} | Runcicantellated 7-cube (Parsa) | (0,0,1,2,2,2,2)√2 + (1,1,1,1,1,1,1) | 53760 | 13440 | ||||||
| 59 | t0,1,6{4,3,3,3,3,3} | Hexitruncated 7-cube (Putsa) | (0,1,1,1,1,1,2)√2 + (1,1,1,1,1,1,1) | 29568 | 5376 | ||||||
| 60 | t0,1,5{4,3,3,3,3,3} | Pentitruncated 7-cube (Tetsa) | (0,1,1,1,1,2,2)√2 + (1,1,1,1,1,1,1) | 87360 | 13440 | ||||||
| 61 | t0,1,4{4,3,3,3,3,3} | Steritruncated 7-cube (Catsa) | (0,1,1,1,2,2,2)√2 + (1,1,1,1,1,1,1) | 116480 | 17920 | ||||||
| 62 | t0,1,3{4,3,3,3,3,3} | Runcitruncated 7-cube (Petsa) | (0,1,1,2,2,2,2)√2 + (1,1,1,1,1,1,1) | 73920 | 13440 | ||||||
| 63 | t0,1,2{4,3,3,3,3,3} | Cantitruncated 7-cube (Gersa) | (0,1,2,2,2,2,2)√2 + (1,1,1,1,1,1,1) | 18816 | 5376 | ||||||
| 64 | t0,1,2,3{3,3,3,3,3,4} | Runcicantitruncated 7-orthoplex (Gopaz) | (0,1,2,3,4,4,4)√2 | 60480 | 13440 | ||||||
| 65 | t0,1,2,4{3,3,3,3,3,4} | Stericantitruncated 7-orthoplex (Cogarz) | (0,0,1,1,2,3,4)√2 | 241920 | 40320 | ||||||
| 66 | t0,1,3,4{3,3,3,3,3,4} | Steriruncitruncated 7-orthoplex (Captaz) | (0,0,1,2,2,3,4)√2 | 181440 | 40320 | ||||||
| 67 | t0,2,3,4{3,3,3,3,3,4} | Steriruncicantellated 7-orthoplex (Caparz) | (0,0,1,2,3,3,4)√2 | 181440 | 40320 | ||||||
| 68 | t1,2,3,4{3,3,3,3,3,4} | Biruncicantitruncated 7-orthoplex (Gibpaz) | (0,0,1,2,3,4,4)√2 | 161280 | 40320 | ||||||
| 69 | t0,1,2,5{3,3,3,3,3,4} | Penticantitruncated 7-orthoplex (Tograz) | (0,1,1,1,2,3,4)√2 | 295680 | 53760 | ||||||
| 70 | t0,1,3,5{3,3,3,3,3,4} | Pentiruncitruncated 7-orthoplex (Toptaz) | (0,1,1,2,2,3,4)√2 | 443520 | 80640 | ||||||
| 71 | t0,2,3,5{3,3,3,3,3,4} | Pentiruncicantellated 7-orthoplex (Toparz) | (0,1,1,2,3,3,4)√2 | 403200 | 80640 | ||||||
| 72 | t1,2,3,5{3,3,3,3,3,4} | Bistericantitruncated 7-orthoplex (Becogarz) | (0,1,1,2,3,4,4)√2 | 362880 | 80640 | ||||||
| 73 | t0,1,4,5{3,3,3,3,3,4} | Pentisteritruncated 7-orthoplex (Tacotaz) | (0,1,2,2,2,3,4)√2 | 241920 | 53760 | ||||||
| 74 | t0,2,4,5{3,3,3,3,3,4} | Pentistericantellated 7-orthoplex (Tocarz) | (0,1,2,2,3,3,4)√2 | 403200 | 80640 | ||||||
| 75 | t1,2,4,5{4,3,3,3,3,3} | Bisteriruncitruncated 7-cube (Bocaptosaz) | (0,1,2,2,3,4,4)√2 | 322560 | 80640 | ||||||
| 76 | t0,3,4,5{3,3,3,3,3,4} | Pentisteriruncinated 7-orthoplex (Tecpaz) | (0,1,2,3,3,3,4)√2 | 241920 | 53760 | ||||||
| 77 | t1,2,3,5{4,3,3,3,3,3} | Bistericantitruncated 7-cube (Becgresa) | (0,1,2,3,3,4,4)√2 | 362880 | 80640 | ||||||
| 78 | t1,2,3,4{4,3,3,3,3,3} | Biruncicantitruncated 7-cube (Gibposa) | (0,1,2,3,4,4,4)√2 | 188160 | 53760 | ||||||
| 79 | t0,1,2,6{3,3,3,3,3,4} | Hexicantitruncated 7-orthoplex (Pugarez) | (0,0,0,0,1,2,3)√2 + (1,1,1,1,1,1,1) | 134400 | 26880 | ||||||
| 80 | t0,1,3,6{3,3,3,3,3,4} | Hexiruncitruncated 7-orthoplex (Papataz) | (0,0,0,1,1,2,3)√2 + (1,1,1,1,1,1,1) | 322560 | 53760 | ||||||
| 81 | t0,2,3,6{3,3,3,3,3,4} | Hexiruncicantellated 7-orthoplex (Puparez) | (0,0,0,1,2,2,3)√2 + (1,1,1,1,1,1,1) | 268800 | 53760 | ||||||
| 82 | t0,3,4,5{4,3,3,3,3,3} | Pentisteriruncinated 7-cube (Tecpasa) | (0,0,0,1,2,3,3)√2 + (1,1,1,1,1,1,1) | 241920 | 53760 | ||||||
| 83 | t0,1,4,6{3,3,3,3,3,4} | Hexisteritruncated 7-orthoplex (Pucotaz) | (0,0,1,1,1,2,3)√2 + (1,1,1,1,1,1,1) | 322560 | 53760 | ||||||
| 84 | t0,2,4,6{4,3,3,3,3,3} | Hexistericantellated 7-cube (Pucrosaz) | (0,0,1,1,2,2,3)√2 + (1,1,1,1,1,1,1) | 483840 | 80640 | ||||||
| 85 | t0,2,4,5{4,3,3,3,3,3} | Pentistericantellated 7-cube (Tecresa) | (0,0,1,1,2,3,3)√2 + (1,1,1,1,1,1,1) | 403200 | 80640 | ||||||
| 86 | t0,2,3,6{4,3,3,3,3,3} | Hexiruncicantellated 7-cube (Pupresa) | (0,0,1,2,2,2,3)√2 + (1,1,1,1,1,1,1) | 268800 | 53760 | ||||||
| 87 | t0,2,3,5{4,3,3,3,3,3} | Pentiruncicantellated 7-cube (Topresa) | (0,0,1,2,2,3,3)√2 + (1,1,1,1,1,1,1) | 403200 | 80640 | ||||||
| 88 | t0,2,3,4{4,3,3,3,3,3} | Steriruncicantellated 7-cube (Copresa) | (0,0,1,2,3,3,3)√2 + (1,1,1,1,1,1,1) | 215040 | 53760 | ||||||
| 89 | t0,1,5,6{4,3,3,3,3,3} | Hexipentitruncated 7-cube (Putatosez) | (0,1,1,1,1,2,3)√2 + (1,1,1,1,1,1,1) | 134400 | 26880 | ||||||
| 90 | t0,1,4,6{4,3,3,3,3,3} | Hexisteritruncated 7-cube (Pacutsa) | (0,1,1,1,2,2,3)√2 + (1,1,1,1,1,1,1) | 322560 | 53760 | ||||||
| 91 | t0,1,4,5{4,3,3,3,3,3} | Pentisteritruncated 7-cube (Tecatsa) | (0,1,1,1,2,3,3)√2 + (1,1,1,1,1,1,1) | 241920 | 53760 | ||||||
| 92 | t0,1,3,6{4,3,3,3,3,3} | Hexiruncitruncated 7-cube (Pupetsa) | (0,1,1,2,2,2,3)√2 + (1,1,1,1,1,1,1) | 322560 | 53760 | ||||||
| 93 | t0,1,3,5{4,3,3,3,3,3} | Pentiruncitruncated 7-cube (Toptosa) | (0,1,1,2,2,3,3)√2 + (1,1,1,1,1,1,1) | 443520 | 80640 | ||||||
| 94 | t0,1,3,4{4,3,3,3,3,3} | Steriruncitruncated 7-cube (Captesa) | (0,1,1,2,3,3,3)√2 + (1,1,1,1,1,1,1) | 215040 | 53760 | ||||||
| 95 | t0,1,2,6{4,3,3,3,3,3} | Hexicantitruncated 7-cube (Pugrosa) | (0,1,2,2,2,2,3)√2 + (1,1,1,1,1,1,1) | 134400 | 26880 | ||||||
| 96 | t0,1,2,5{4,3,3,3,3,3} | Penticantitruncated 7-cube (Togresa) | (0,1,2,2,2,3,3)√2 + (1,1,1,1,1,1,1) | 295680 | 53760 | ||||||
| 97 | t0,1,2,4{4,3,3,3,3,3} | Stericantitruncated 7-cube (Cogarsa) | (0,1,2,2,3,3,3)√2 + (1,1,1,1,1,1,1) | 268800 | 53760 | ||||||
| 98 | t0,1,2,3{4,3,3,3,3,3} | Runcicantitruncated 7-cube (Gapsa) | (0,1,2,3,3,3,3)√2 + (1,1,1,1,1,1,1) | 94080 | 26880 | ||||||
| 99 | t0,1,2,3,4{3,3,3,3,3,4} | Steriruncicantitruncated 7-orthoplex (Gocaz) | (0,0,1,2,3,4,5)√2 | 322560 | 80640 | ||||||
| 100 | t0,1,2,3,5{3,3,3,3,3,4} | Pentiruncicantitruncated 7-orthoplex (Tegopaz) | (0,1,1,2,3,4,5)√2 | 725760 | 161280 | ||||||
| 101 | t0,1,2,4,5{3,3,3,3,3,4} | Pentistericantitruncated 7-orthoplex (Tecagraz) | (0,1,2,2,3,4,5)√2 | 645120 | 161280 | ||||||
| 102 | t0,1,3,4,5{3,3,3,3,3,4} | Pentisteriruncitruncated 7-orthoplex (Tecpotaz) | (0,1,2,3,3,4,5)√2 | 645120 | 161280 | ||||||
| 103 | t0,2,3,4,5{3,3,3,3,3,4} | Pentisteriruncicantellated 7-orthoplex (Tacparez) | (0,1,2,3,4,4,5)√2 | 645120 | 161280 | ||||||
| 104 | t1,2,3,4,5{4,3,3,3,3,3} | Bisteriruncicantitruncated 7-cube (Gabcosaz) | (0,1,2,3,4,5,5)√2 | 564480 | 161280 | ||||||
| 105 | t0,1,2,3,6{3,3,3,3,3,4} | Hexiruncicantitruncated 7-orthoplex (Pugopaz) | (0,0,0,1,2,3,4)√2 + (1,1,1,1,1,1,1) | 483840 | 107520 | ||||||
| 106 | t0,1,2,4,6{3,3,3,3,3,4} | Hexistericantitruncated 7-orthoplex (Pucagraz) | (0,0,1,1,2,3,4)√2 + (1,1,1,1,1,1,1) | 806400 | 161280 | ||||||
| 107 | t0,1,3,4,6{3,3,3,3,3,4} | Hexisteriruncitruncated 7-orthoplex (Pucpotaz) | (0,0,1,2,2,3,4)√2 + (1,1,1,1,1,1,1) | 725760 | 161280 | ||||||
| 108 | t0,2,3,4,6{4,3,3,3,3,3} | Hexisteriruncicantellated 7-cube (Pucprosaz) | (0,0,1,2,3,3,4)√2 + (1,1,1,1,1,1,1) | 725760 | 161280 | ||||||
| 109 | t0,2,3,4,5{4,3,3,3,3,3} | Pentisteriruncicantellated 7-cube (Tocpresa) | (0,0,1,2,3,4,4)√2 + (1,1,1,1,1,1,1) | 645120 | 161280 | ||||||
| 110 | t0,1,2,5,6{3,3,3,3,3,4} | Hexipenticantitruncated 7-orthoplex (Putegraz) | (0,1,1,1,2,3,4)√2 + (1,1,1,1,1,1,1) | 483840 | 107520 | ||||||
| 111 | t0,1,3,5,6{4,3,3,3,3,3} | Hexipentiruncitruncated 7-cube (Putpetsaz) | (0,1,1,2,2,3,4)√2 + (1,1,1,1,1,1,1) | 806400 | 161280 | ||||||
| 112 | t0,1,3,4,6{4,3,3,3,3,3} | Hexisteriruncitruncated 7-cube (Pucpetsa) | (0,1,1,2,3,3,4)√2 + (1,1,1,1,1,1,1) | 725760 | 161280 | ||||||
| 113 | t0,1,3,4,5{4,3,3,3,3,3} | Pentisteriruncitruncated 7-cube (Tecpetsa) | (0,1,1,2,3,4,4)√2 + (1,1,1,1,1,1,1) | 645120 | 161280 | ||||||
| 114 | t0,1,2,5,6{4,3,3,3,3,3} | Hexipenticantitruncated 7-cube (Putgresa) | (0,1,2,2,2,3,4)√2 + (1,1,1,1,1,1,1) | 483840 | 107520 | ||||||
| 115 | t0,1,2,4,6{4,3,3,3,3,3} | Hexistericantitruncated 7-cube (Pucagrosa) | (0,1,2,2,3,3,4)√2 + (1,1,1,1,1,1,1) | 806400 | 161280 | ||||||
| 116 | t0,1,2,4,5{4,3,3,3,3,3} | Pentistericantitruncated 7-cube (Tecgresa) | (0,1,2,2,3,4,4)√2 + (1,1,1,1,1,1,1) | 645120 | 161280 | ||||||
| 117 | t0,1,2,3,6{4,3,3,3,3,3} | Hexiruncicantitruncated 7-cube (Pugopsa) | (0,1,2,3,3,3,4)√2 + (1,1,1,1,1,1,1) | 483840 | 107520 | ||||||
| 118 | t0,1,2,3,5{4,3,3,3,3,3} | Pentiruncicantitruncated 7-cube (Togapsa) | (0,1,2,3,3,4,4)√2 + (1,1,1,1,1,1,1) | 725760 | 161280 | ||||||
| 119 | t0,1,2,3,4{4,3,3,3,3,3} | Steriruncicantitruncated 7-cube (Gacosa) | (0,1,2,3,4,4,4)√2 + (1,1,1,1,1,1,1) | 376320 | 107520 | ||||||
| 120 | t0,1,2,3,4,5{3,3,3,3,3,4} | Pentisteriruncicantitruncated 7-orthoplex (Gotaz) | (0,1,2,3,4,5,6)√2 | 1128960 | 322560 | ||||||
| 121 | t0,1,2,3,4,6{3,3,3,3,3,4} | Hexisteriruncicantitruncated 7-orthoplex (Pugacaz) | (0,0,1,2,3,4,5)√2 + (1,1,1,1,1,1,1) | 1290240 | 322560 | ||||||
| 122 | t0,1,2,3,5,6{3,3,3,3,3,4} | Hexipentiruncicantitruncated 7-orthoplex (Putgapaz) | (0,1,1,2,3,4,5)√2 + (1,1,1,1,1,1,1) | 1290240 | 322560 | ||||||
| 123 | t0,1,2,4,5,6{4,3,3,3,3,3} | Hexipentistericantitruncated 7-cube (Putcagrasaz) | (0,1,2,2,3,4,5)√2 + (1,1,1,1,1,1,1) | 1290240 | 322560 | ||||||
| 124 | t0,1,2,3,5,6{4,3,3,3,3,3} | Hexipentiruncicantitruncated 7-cube (Putgapsa) | (0,1,2,3,3,4,5)√2 + (1,1,1,1,1,1,1) | 1290240 | 322560 | ||||||
| 125 | t0,1,2,3,4,6{4,3,3,3,3,3} | Hexisteriruncicantitruncated 7-cube (Pugacasa) | (0,1,2,3,4,4,5)√2 + (1,1,1,1,1,1,1) | 1290240 | 322560 | ||||||
| 126 | t0,1,2,3,4,5{4,3,3,3,3,3} | Pentisteriruncicantitruncated 7-cube (Gotesa) | (0,1,2,3,4,5,5)√2 + (1,1,1,1,1,1,1) | 1128960 | 322560 | ||||||
| 127 | t0,1,2,3,4,5,6{4,3,3,3,3,3} | Omnitruncated 7-cube (Guposaz) | (0,1,2,3,4,5,6)√2 + (1,1,1,1,1,1,1) | 2257920 | 645120 | ||||||
The D7 family
The D7 family has symmetry of order 322560 (7 factorial x 26).
This family has 3×32−1=95 Wythoffian uniform polytopes, generated by marking one or more nodes of the D7 Coxeter-Dynkin diagram. Of these, 63 (2×32−1) are repeated from the B7 family and 32 are unique to this family, listed below. Bowers names and acronym are given for cross-referencing.
See also list of D7 polytopes for Coxeter plane graphs of these polytopes.
| D7 uniform polytopes | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| # | Coxeter diagram | Names | Base point (Alternately signed) |
Element counts | |||||||
| 6 | 5 | 4 | 3 | 2 | 1 | 0 | |||||
| 1 | 7-cube demihepteract (hesa) | (1,1,1,1,1,1,1) | 78 | 532 | 1624 | 2800 | 2240 | 672 | 64 | ||
| 2 | cantic 7-cube truncated demihepteract (thesa) | (1,1,3,3,3,3,3) | 142 | 1428 | 5656 | 11760 | 13440 | 7392 | 1344 | ||
| 3 | runcic 7-cube small rhombated demihepteract (sirhesa) | (1,1,1,3,3,3,3) | 16800 | 2240 | |||||||
| 4 | steric 7-cube small prismated demihepteract (sphosa) | (1,1,1,1,3,3,3) | 20160 | 2240 | |||||||
| 5 | pentic 7-cube small cellated demihepteract (sochesa) | (1,1,1,1,1,3,3) | 13440 | 1344 | |||||||
| 6 | hexic 7-cube small terated demihepteract (suthesa) | (1,1,1,1,1,1,3) | 4704 | 448 | |||||||
| 7 | runcicantic 7-cube great rhombated demihepteract (Girhesa) | (1,1,3,5,5,5,5) | 23520 | 6720 | |||||||
| 8 | stericantic 7-cube prismatotruncated demihepteract (pothesa) | (1,1,3,3,5,5,5) | 73920 | 13440 | |||||||
| 9 | steriruncic 7-cube prismatorhomated demihepteract (prohesa) | (1,1,1,3,5,5,5) | 40320 | 8960 | |||||||
| 10 | penticantic 7-cube cellitruncated demihepteract (cothesa) | (1,1,3,3,3,5,5) | 87360 | 13440 | |||||||
| 11 | pentiruncic 7-cube cellirhombated demihepteract (crohesa) | (1,1,1,3,3,5,5) | 87360 | 13440 | |||||||
| 12 | pentisteric 7-cube celliprismated demihepteract (caphesa) | (1,1,1,1,3,5,5) | 40320 | 6720 | |||||||
| 13 | hexicantic 7-cube tericantic demihepteract (tuthesa) | (1,1,3,3,3,3,5) | 43680 | 6720 | |||||||
| 14 | hexiruncic 7-cube terirhombated demihepteract (turhesa) | (1,1,1,3,3,3,5) | 67200 | 8960 | |||||||
| 15 | hexisteric 7-cube teriprismated demihepteract (tuphesa) | (1,1,1,1,3,3,5) | 53760 | 6720 | |||||||
| 16 | hexipentic 7-cube tericellated demihepteract (tuchesa) | (1,1,1,1,1,3,5) | 21504 | 2688 | |||||||
| 17 | steriruncicantic 7-cube great prismated demihepteract (Gephosa) | (1,1,3,5,7,7,7) | 94080 | 26880 | |||||||
| 18 | pentiruncicantic 7-cube celligreatorhombated demihepteract (cagrohesa) | (1,1,3,5,5,7,7) | 181440 | 40320 | |||||||
| 19 | pentistericantic 7-cube celliprismatotruncated demihepteract (capthesa) | (1,1,3,3,5,7,7) | 181440 | 40320 | |||||||
| 20 | pentisteriruncic 7-cube celliprismatorhombated demihepteract (coprahesa) | (1,1,1,3,5,7,7) | 120960 | 26880 | |||||||
| 21 | hexiruncicantic 7-cube terigreatorhombated demihepteract (tugrohesa) | (1,1,3,5,5,5,7) | 120960 | 26880 | |||||||
| 22 | hexistericantic 7-cube teriprismatotruncated demihepteract (tupthesa) | (1,1,3,3,5,5,7) | 221760 | 40320 | |||||||
| 23 | hexisteriruncic 7-cube teriprismatorhombated demihepteract (tuprohesa) | (1,1,1,3,5,5,7) | 134400 | 26880 | |||||||
| 24 | hexipenticantic 7-cube teriCellitruncated demihepteract (tucothesa) | (1,1,3,3,3,5,7) | 147840 | 26880 | |||||||
| 25 | hexipentiruncic 7-cube tericellirhombated demihepteract (tucrohesa) | (1,1,1,3,3,5,7) | 161280 | 26880 | |||||||
| 26 | hexipentisteric 7-cube tericelliprismated demihepteract (tucophesa) | (1,1,1,1,3,5,7) | 80640 | 13440 | |||||||
| 27 | pentisteriruncicantic 7-cube great cellated demihepteract (gochesa) | (1,1,3,5,7,9,9) | 282240 | 80640 | |||||||
| 28 | hexisteriruncicantic 7-cube terigreatoprimated demihepteract (tugphesa) | (1,1,3,5,7,7,9) | 322560 | 80640 | |||||||
| 29 | hexipentiruncicantic 7-cube tericelligreatorhombated demihepteract (tucagrohesa) | (1,1,3,5,5,7,9) | 322560 | 80640 | |||||||
| 30 | hexipentistericantic 7-cube tericelliprismatotruncated demihepteract (tucpathesa) | (1,1,3,3,5,7,9) | 362880 | 80640 | |||||||
| 31 | hexipentisteriruncic 7-cube tericellprismatorhombated demihepteract (tucprohesa) | (1,1,1,3,5,7,9) | 241920 | 53760 | |||||||
| 32 | hexipentisteriruncicantic 7-cube great terated demihepteract (guthesa) | (1,1,3,5,7,9,11) | 564480 | 161280 | |||||||
The E7 family
The E7 Coxeter group has order 2,903,040.
There are 127 forms based on all permutations of the Coxeter-Dynkin diagrams with one or more rings.
See also a list of E7 polytopes for symmetric Coxeter plane graphs of these polytopes.
| E7 uniform polytopes | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| # | Coxeter-Dynkin diagram Schläfli symbol |
Names | Element counts | ||||||||
| 6 | 5 | 4 | 3 | 2 | 1 | 0 | |||||
| 1 | 231 (laq) | 632 | 4788 | 16128 | 20160 | 10080 | 2016 | 126 | |||
| 2 | Rectified 231 (rolaq) | 758 | 10332 | 47880 | 100800 | 90720 | 30240 | 2016 | |||
| 3 | Rectified 132 (rolin) | 758 | 12348 | 72072 | 191520 | 241920 | 120960 | 10080 | |||
| 4 | 132 (lin) | 182 | 4284 | 23688 | 50400 | 40320 | 10080 | 576 | |||
| 5 | Birectified 321 (branq) | 758 | 12348 | 68040 | 161280 | 161280 | 60480 | 4032 | |||
| 6 | Rectified 321 (ranq) | 758 | 44352 | 70560 | 48384 | 11592 | 12096 | 756 | |||
| 7 | 321 (naq) | 702 | 6048 | 12096 | 10080 | 4032 | 756 | 56 | |||
| 8 | Truncated 231 (talq) | 758 | 10332 | 47880 | 100800 | 90720 | 32256 | 4032 | |||
| 9 | Cantellated 231 (sirlaq) | 131040 | 20160 | ||||||||
| 10 | Bitruncated 231 (botlaq) | 30240 | |||||||||
| 11 | small demified 231 (shilq) | 2774 | 22428 | 78120 | 151200 | 131040 | 42336 | 4032 | |||
| 12 | demirectified 231 (hirlaq) | 12096 | |||||||||
| 13 | truncated 132 (tolin) | 20160 | |||||||||
| 14 | small demiprismated 231 (shiplaq) | 20160 | |||||||||
| 15 | birectified 132 (berlin) | 758 | 22428 | 142632 | 403200 | 544320 | 302400 | 40320 | |||
| 16 | tritruncated 321 (totanq) | 40320 | |||||||||
| 17 | demibirectified 321 (hobranq) | 20160 | |||||||||
| 18 | small cellated 231 (scalq) | 7560 | |||||||||
| 19 | small biprismated 231 (sobpalq) | 30240 | |||||||||
| 20 | small birhombated 321 (sabranq) | 60480 | |||||||||
| 21 | demirectified 321 (harnaq) | 12096 | |||||||||
| 22 | bitruncated 321 (botnaq) | 12096 | |||||||||
| 23 | small terated 321 (stanq) | 1512 | |||||||||
| 24 | small demicellated 321 (shocanq) | 12096 | |||||||||
| 25 | small prismated 321 (spanq) | 40320 | |||||||||
| 26 | small demified 321 (shanq) | 4032 | |||||||||
| 27 | small rhombated 321 (sranq) | 12096 | |||||||||
| 28 | Truncated 321 (tanq) | 758 | 11592 | 48384 | 70560 | 44352 | 12852 | 1512 | |||
| 29 | great rhombated 231 (girlaq) | 60480 | |||||||||
| 30 | demitruncated 231 (hotlaq) | 24192 | |||||||||
| 31 | small demirhombated 231 (sherlaq) | 60480 | |||||||||
| 32 | demibitruncated 231 (hobtalq) | 60480 | |||||||||
| 33 | demiprismated 231 (hiptalq) | 80640 | |||||||||
| 34 | demiprismatorhombated 231 (hiprolaq) | 120960 | |||||||||
| 35 | bitruncated 132 (batlin) | 120960 | |||||||||
| 36 | small prismated 231 (spalq) | 80640 | |||||||||
| 37 | small rhombated 132 (sirlin) | 120960 | |||||||||
| 38 | tritruncated 231 (tatilq) | 80640 | |||||||||
| 39 | cellitruncated 231 (catalaq) | 60480 | |||||||||
| 40 | cellirhombated 231 (crilq) | 362880 | |||||||||
| 41 | biprismatotruncated 231 (biptalq) | 181440 | |||||||||
| 42 | small prismated 132 (seplin) | 60480 | |||||||||
| 43 | small biprismated 321 (sabipnaq) | 120960 | |||||||||
| 44 | small demibirhombated 321 (shobranq) | 120960 | |||||||||
| 45 | cellidemiprismated 231 (chaplaq) | 60480 | |||||||||
| 46 | demibiprismatotruncated 321 (hobpotanq) | 120960 | |||||||||
| 47 | great birhombated 321 (gobranq) | 120960 | |||||||||
| 48 | demibitruncated 321 (hobtanq) | 60480 | |||||||||
| 49 | teritruncated 231 (totalq) | 24192 | |||||||||
| 50 | terirhombated 231 (trilq) | 120960 | |||||||||
| 51 | demicelliprismated 321 (hicpanq) | 120960 | |||||||||
| 52 | small teridemified 231 (sethalq) | 24192 | |||||||||
| 53 | small cellated 321 (scanq) | 60480 | |||||||||
| 54 | demiprismated 321 (hipnaq) | 80640 | |||||||||
| 55 | terirhombated 321 (tranq) | 60480 | |||||||||
| 56 | demicellirhombated 321 (hocranq) | 120960 | |||||||||
| 57 | prismatorhombated 321 (pranq) | 120960 | |||||||||
| 58 | small demirhombated 321 (sharnaq) | 60480 | |||||||||
| 59 | teritruncated 321 (tetanq) | 15120 | |||||||||
| 60 | demicellitruncated 321 (hictanq) | 60480 | |||||||||
| 61 | prismatotruncated 321 (potanq) | 120960 | |||||||||
| 62 | demitruncated 321 (hotnaq) | 24192 | |||||||||
| 63 | great rhombated 321 (granq) | 24192 | |||||||||
| 64 | great demified 231 (gahlaq) | 120960 | |||||||||
| 65 | great demiprismated 231 (gahplaq) | 241920 | |||||||||
| 66 | prismatotruncated 231 (potlaq) | 241920 | |||||||||
| 67 | prismatorhombated 231 (prolaq) | 241920 | |||||||||
| 68 | great rhombated 132 (girlin) | 241920 | |||||||||
| 69 | celligreatorhombated 231 (cagrilq) | 362880 | |||||||||
| 70 | cellidemitruncated 231 (chotalq) | 241920 | |||||||||
| 71 | prismatotruncated 132 (patlin) | 362880 | |||||||||
| 72 | biprismatorhombated 321 (bipirnaq) | 362880 | |||||||||
| 73 | tritruncated 132 (tatlin) | 241920 | |||||||||
| 74 | cellidemiprismatorhombated 231 (chopralq) | 362880 | |||||||||
| 75 | great demibiprismated 321 (ghobipnaq) | 362880 | |||||||||
| 76 | celliprismated 231 (caplaq) | 241920 | |||||||||
| 77 | biprismatotruncated 321 (boptanq) | 362880 | |||||||||
| 78 | great trirhombated 231 (gatralaq) | 241920 | |||||||||
| 79 | terigreatorhombated 231 (togrilq) | 241920 | |||||||||
| 80 | teridemitruncated 231 (thotalq) | 120960 | |||||||||
| 81 | teridemirhombated 231 (thorlaq) | 241920 | |||||||||
| 82 | celliprismated 321 (capnaq) | 241920 | |||||||||
| 83 | teridemiprismatotruncated 231 (thoptalq) | 241920 | |||||||||
| 84 | teriprismatorhombated 321 (tapronaq) | 362880 | |||||||||
| 85 | demicelliprismatorhombated 321 (hacpranq) | 362880 | |||||||||
| 86 | teriprismated 231 (toplaq) | 241920 | |||||||||
| 87 | cellirhombated 321 (cranq) | 362880 | |||||||||
| 88 | demiprismatorhombated 321 (hapranq) | 241920 | |||||||||
| 89 | tericellitruncated 231 (tectalq) | 120960 | |||||||||
| 90 | teriprismatotruncated 321 (toptanq) | 362880 | |||||||||
| 91 | demicelliprismatotruncated 321 (hecpotanq) | 362880 | |||||||||
| 92 | teridemitruncated 321 (thotanq) | 120960 | |||||||||
| 93 | cellitruncated 321 (catnaq) | 241920 | |||||||||
| 94 | demiprismatotruncated 321 (hiptanq) | 241920 | |||||||||
| 95 | terigreatorhombated 321 (tagranq) | 120960 | |||||||||
| 96 | demicelligreatorhombated 321 (hicgarnq) | 241920 | |||||||||
| 97 | great prismated 321 (gopanq) | 241920 | |||||||||
| 98 | great demirhombated 321 (gahranq) | 120960 | |||||||||
| 99 | great prismated 231 (gopalq) | 483840 | |||||||||
| 100 | great cellidemified 231 (gechalq) | 725760 | |||||||||
| 101 | great birhombated 132 (gebrolin) | 725760 | |||||||||
| 102 | prismatorhombated 132 (prolin) | 725760 | |||||||||
| 103 | celliprismatorhombated 231 (caprolaq) | 725760 | |||||||||
| 104 | great biprismated 231 (gobpalq) | 725760 | |||||||||
| 105 | tericelliprismated 321 (ticpanq) | 483840 | |||||||||
| 106 | teridemigreatoprismated 231 (thegpalq) | 725760 | |||||||||
| 107 | teriprismatotruncated 231 (teptalq) | 725760 | |||||||||
| 108 | teriprismatorhombated 231 (topralq) | 725760 | |||||||||
| 109 | cellipriemsatorhombated 321 (copranq) | 725760 | |||||||||
| 110 | tericelligreatorhombated 231 (tecgrolaq) | 725760 | |||||||||
| 111 | tericellitruncated 321 (tectanq) | 483840 | |||||||||
| 112 | teridemiprismatotruncated 321 (thoptanq) | 725760 | |||||||||
| 113 | celliprismatotruncated 321 (coptanq) | 725760 | |||||||||
| 114 | teridemicelligreatorhombated 321 (thocgranq) | 483840 | |||||||||
| 115 | terigreatoprismated 321 (tagpanq) | 725760 | |||||||||
| 116 | great demicellated 321 (gahcnaq) | 725760 | |||||||||
| 117 | tericelliprismated laq (tecpalq) | 483840 | |||||||||
| 118 | celligreatorhombated 321 (cogranq) | 725760 | |||||||||
| 119 | great demified 321 (gahnq) | 483840 | |||||||||
| 120 | great cellated 231 (gocalq) | 1451520 | |||||||||
| 121 | terigreatoprismated 231 (tegpalq) | 1451520 | |||||||||
| 122 | tericelliprismatotruncated 321 (tecpotniq) | 1451520 | |||||||||
| 123 | tericellidemigreatoprismated 231 (techogaplaq) | 1451520 | |||||||||
| 124 | tericelligreatorhombated 321 (tacgarnq) | 1451520 | |||||||||
| 125 | tericelliprismatorhombated 231 (tecprolaq) | 1451520 | |||||||||
| 126 | great cellated 321 (gocanq) | 1451520 | |||||||||
| 127 | great terated 321 (gotanq) | 2903040 | |||||||||
Regular and uniform honeycombs

There are five fundamental affine Coxeter groups and sixteen prismatic groups that generate regular and uniform tessellations in 6-space:
| # | Coxeter group | Coxeter diagram | Forms | |
|---|---|---|---|---|
| 1 | [3[7]] | 17 | ||
| 2 | [4,34,4] | 71 | ||
| 3 | h[4,34,4] [4,33,31,1] | 95 (32 new) | ||
| 4 | q[4,34,4] [31,1,32,31,1] | 41 (6 new) | ||
| 5 | [32,2,2] | 39 | ||
Regular and uniform tessellations include:
- , 17 forms
- Uniform 6-simplex honeycomb: {3[7]}







- Uniform Cyclotruncated 6-simplex honeycomb: t0,1{3[7]}







- Uniform Omnitruncated 6-simplex honeycomb: t0,1,2,3,4,5,6,7{3[7]}




- Uniform 6-simplex honeycomb: {3[7]}
- , [4,34,4], 71 forms
- Regular 6-cube honeycomb, represented by symbols {4,34,4},













- Regular 6-cube honeycomb, represented by symbols {4,34,4},
- , [31,1,33,4], 95 forms, 64 shared with , 32 new
- Uniform 6-demicube honeycomb, represented by symbols h{4,34,4} = {31,1,33,4},












 =
= 









- Uniform 6-demicube honeycomb, represented by symbols h{4,34,4} = {31,1,33,4},
- , [31,1,32,31,1], 41 unique ringed permutations, most shared with and , and 6 are new. Coxeter calls the first one a quarter 6-cubic honeycomb.
-





 =
= 












-





 =
= 












-





 =
= 












-





 =
= 












-





 =
= 












-





 =
= 












-
- : [32,2,2], 39 forms
- Uniform 222 honeycomb: represented by symbols {3,3,32,2},








- Uniform t4(222) honeycomb: 4r{3,3,32,2},







- Uniform 0222 honeycomb: {32,2,2},








- Uniform t2(0222) honeycomb: 2r{32,2,2},







- Uniform 222 honeycomb: represented by symbols {3,3,32,2},
| # | Coxeter group | Coxeter-Dynkin diagram | |
|---|---|---|---|
| 1 | x | [3[6],2,∞] | |
| 2 | x | [4,3,31,1,2,∞] | |
| 3 | x | [4,33,4,2,∞] | |
| 4 | x | [31,1,3,31,1,2,∞] | |
| 5 | xx | [3[5],2,∞,2,∞,2,∞] | |
| 6 | xx | [4,3,31,1,2,∞,2,∞] | |
| 7 | xx | [4,3,3,4,2,∞,2,∞] | |
| 8 | xx | [31,1,1,1,2,∞,2,∞] | |
| 9 | xx | [3,4,3,3,2,∞,2,∞] | |
| 10 | xxx | [4,3,4,2,∞,2,∞,2,∞] | |
| 11 | xxx | [4,31,1,2,∞,2,∞,2,∞] | |
| 12 | xxx | [3[4],2,∞,2,∞,2,∞] | |
| 13 | xxxx | [4,4,2,∞,2,∞,2,∞,2,∞] | |
| 14 | xxxx | [6,3,2,∞,2,∞,2,∞,2,∞] | |
| 15 | xxxx | [3[3],2,∞,2,∞,2,∞,2,∞] | |
| 16 | xxxxx | [∞,2,∞,2,∞,2,∞,2,∞] | |
Regular and uniform hyperbolic honeycombs
There are no compact hyperbolic Coxeter groups of rank 7, groups that can generate honeycombs with all finite facets, and a finite vertex figure. However, there are 3 noncompact hyperbolic Coxeter groups of rank 7, each generating uniform honeycombs in 6-space as permutations of rings of the Coxeter diagrams.
| = [3,3[6]]: |
= [31,1,3,32,1]: |
= [4,3,3,32,1]: |
Notes on the Wythoff construction for the uniform 7-polytopes
The reflective 7-dimensional uniform polytopes are constructed through a Wythoff construction process, and represented by a Coxeter-Dynkin diagram, where each node represents a mirror. An active mirror is represented by a ringed node. Each combination of active mirrors generates a unique uniform polytope. Uniform polytopes are named in relation to the regular polytopes in each family. Some families have two regular constructors and thus may be named in two equally valid ways.
Here are the primary operators available for constructing and naming the uniform 7-polytopes.
The prismatic forms and bifurcating graphs can use the same truncation indexing notation, but require an explicit numbering system on the nodes for clarity.
| Operation | Extended Schläfli symbol |
Coxeter- Dynkin diagram |
Description |
|---|---|---|---|
| Parent | t0{p,q,r,s,t,u} | Any regular 7-polytope | |
| Rectified | t1{p,q,r,s,t,u} | The edges are fully truncated into single points. The 7-polytope now has the combined faces of the parent and dual. | |
| Birectified | t2{p,q,r,s,t,u} | Birectification reduces cells to their duals. | |
| Truncated | t0,1{p,q,r,s,t,u} | Each original vertex is cut off, with a new face filling the gap. Truncation has a degree of freedom, which has one solution that creates a uniform truncated 7-polytope. The 7-polytope has its original faces doubled in sides, and contains the faces of the dual.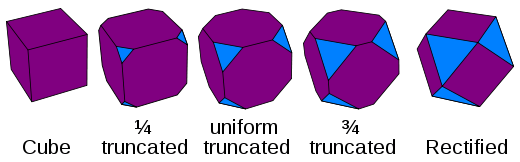 | |
| Bitruncated | t1,2{p,q,r,s,t,u} | Bitrunction transforms cells to their dual truncation. | |
| Tritruncated | t2,3{p,q,r,s,t,u} | Tritruncation transforms 4-faces to their dual truncation. | |
| Cantellated | t0,2{p,q,r,s,t,u} | In addition to vertex truncation, each original edge is beveled with new rectangular faces appearing in their place. A uniform cantellation is half way between both the parent and dual forms.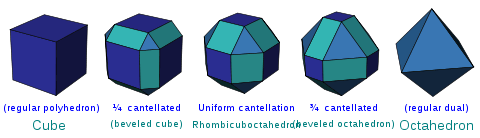 | |
| Bicantellated | t1,3{p,q,r,s,t,u} | In addition to vertex truncation, each original edge is beveled with new rectangular faces appearing in their place. A uniform cantellation is half way between both the parent and dual forms. | |
| Runcinated | t0,3{p,q,r,s,t,u} | Runcination reduces cells and creates new cells at the vertices and edges. | |
| Biruncinated | t1,4{p,q,r,s,t,u} | Runcination reduces cells and creates new cells at the vertices and edges. | |
| Stericated | t0,4{p,q,r,s,t,u} | Sterication reduces 4-faces and creates new 4-faces at the vertices, edges, and faces in the gaps. | |
| Pentellated | t0,5{p,q,r,s,t,u} | Pentellation reduces 5-faces and creates new 5-faces at the vertices, edges, faces, and cells in the gaps. | |
| Hexicated | t0,6{p,q,r,s,t,u} | Hexication reduces 6-faces and creates new 6-faces at the vertices, edges, faces, cells, and 4-faces in the gaps. (expansion operation for 7-polytopes) | |
| Omnitruncated | t0,1,2,3,4,5,6{p,q,r,s,t,u} | All six operators, truncation, cantellation, runcination, sterication, pentellation, and hexication are applied. |
References
- T. Gosset: On the Regular and Semi-Regular Figures in Space of n Dimensions, Messenger of Mathematics, Macmillan, 1900
- A. Boole Stott: Geometrical deduction of semiregular from regular polytopes and space fillings, Verhandelingen of the Koninklijke academy van Wetenschappen width unit Amsterdam, Eerste Sectie 11,1, Amsterdam, 1910
- H.S.M. Coxeter:
- H.S.M. Coxeter, M.S. Longuet-Higgins und J.C.P. Miller: Uniform Polyhedra, Philosophical Transactions of the Royal Society of London, Londne, 1954
- H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 http://www.wiley.com/WileyCDA/WileyTitle/productCd-0471010030.html
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
- Klitzing, Richard. "7D uniform polytopes (polyexa)".
External links
- Polytope names
- Polytopes of Various Dimensions
- Multi-dimensional Glossary
- Glossary for hyperspace, George Olshevsky.
| Fundamental convex regular and uniform polytopes in dimensions 2–10 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Family | An | Bn | I2(p) / Dn | E6 / E7 / E8 / E9 / E10 / F4 / G2 | Hn | |||||||
| Regular polygon | Triangle | Square | p-gon | Hexagon | Pentagon | |||||||
| Uniform polyhedron | Tetrahedron | Octahedron • Cube | Demicube | Dodecahedron • Icosahedron | ||||||||
| Uniform 4-polytope | 5-cell | 16-cell • Tesseract | Demitesseract | 24-cell | 120-cell • 600-cell | |||||||
| Uniform 5-polytope | 5-simplex | 5-orthoplex • 5-cube | 5-demicube | |||||||||
| Uniform 6-polytope | 6-simplex | 6-orthoplex • 6-cube | 6-demicube | 122 • 221 | ||||||||
| Uniform 7-polytope | 7-simplex | 7-orthoplex • 7-cube | 7-demicube | 132 • 231 • 321 | ||||||||
| Uniform 8-polytope | 8-simplex | 8-orthoplex • 8-cube | 8-demicube | 142 • 241 • 421 | ||||||||
| Uniform 9-polytope | 9-simplex | 9-orthoplex • 9-cube | 9-demicube | |||||||||
| Uniform 10-polytope | 10-simplex | 10-orthoplex • 10-cube | 10-demicube | |||||||||
| Uniform n-polytope | n-simplex | n-orthoplex • n-cube | n-demicube | 1k2 • 2k1 • k21 | n-pentagonal polytope | |||||||
| Topics: Polytope families • Regular polytope • List of regular polytopes and compounds | ||||||||||||