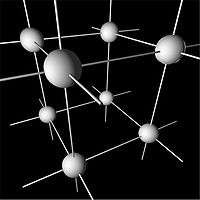
Cubic honeycomb
| Cubic honeycomb | |
|---|---|
  | |
| Type | Regular honeycomb |
| Family | Hypercube honeycomb |
| Indexing[1] | J11,15, A1 W1, G22 |
| Schläfli symbol | {4,3,4} |
| Coxeter diagram | |
| Cell type | {4,3} |
| Face type | {4} |
| Vertex figure | 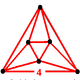 (octahedron) |
| Space group Fibrifold notation | Pm3m (221) 4−:2 |
| Coxeter group | , [4,3,4] |
| Dual | self-dual |
| Properties | vertex-transitive, quasiregular |
The cubic honeycomb or cubic cellulation is the only regular space-filling tessellation (or honeycomb) in Euclidean 3-space, made up of cubic cells. It has 4 cubes around every edge, and 8 cubes around each vertex. Its vertex figure is a regular octahedron. It is a self-dual tessellation with Schläfli symbol {4,3,4}. John Horton Conway calls this honeycomb a cubille.
A geometric honeycomb is a space-filling of polyhedral or higher-dimensional cells, so that there are no gaps. It is an example of the more general mathematical tiling or tessellation in any number of dimensions.
Honeycombs are usually constructed in ordinary Euclidean ("flat") space, like the convex uniform honeycombs. They may also be constructed in non-Euclidean spaces, such as hyperbolic uniform honeycombs. Any finite uniform polytope can be projected to its circumsphere to form a uniform honeycomb in spherical space.
Cartesian coordinates
The Cartesian coordinates of the vertices are:
- (i, j, k)
- for all integral values: i,j,k, with edges parallel to the axes and with an edge length of 1.
Related honeycombs
It is part of a multidimensional family of hypercube honeycombs, with Schläfli symbols of the form {4,3,...,3,4}, starting with the square tiling, {4,4} in the plane.
It is one of 28 uniform honeycombs using convex uniform polyhedral cells.
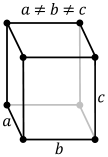
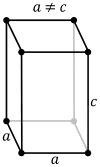
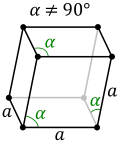
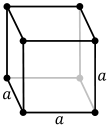
Isometries of simple cubic lattices
Simple cubic lattices can be distorted into lower symmetries, represented by lower crystal systems:
| Crystal system | Monoclinic Triclinic |
Orthorhombic | Tetragonal | Rhombohedral | Cubic |
|---|---|---|---|---|---|
| Unit cell | Parallelepiped | Rectangular cuboid | Square cuboid | Trigonal trapezohedron |
Cube |
| Point group Order Rotation subgroup |
[ ], (*) Order 2 [ ]+, (1) |
[2,2], (*222) Order 8 [2,2]+, (222) |
[4,2], (*422) Order 16 [4,2]+, (422) |
[3], (*33) Order 6 [3]+, (33) |
[4,3], (*432) Order 48 [4,3]+, (432) |
| Diagram |  |
 |
 |
 |
 |
| Space group Rotation subgroup |
Pm (6) P1 (1) |
Pmmm (47) P222 (16) |
P4/mmm (123) P422 (89) |
R3m (160) R3 (146) |
Pm3m (221) P432 (207) |
| Coxeter notation | - | [∞]a×[∞]b×[∞]c | [4,4]a×[∞]c | - | [4,3,4]a |
| Coxeter diagram | - | |
|
- | |
Uniform colorings
There is a large number of uniform colorings, derived from different symmetries. These include:
| Coxeter notation Space group |
Coxeter diagram | Schläfli symbol | Partial honeycomb |
Colors by letters |
|---|---|---|---|---|
| [4,3,4] Pm3m (221) |
{4,3,4} |  |
1: aaaa/aaaa | |
| [4,31,1] = [4,3,4,1+] Fm3m (225) |
{4,31,1} | |
2: abba/baab | |
| [4,3,4] Pm3m (221) |
t0,3{4,3,4} | 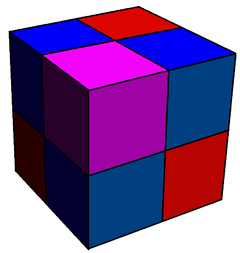 |
4: abbc/bccd | |
| [[4,3,4]] Pm3m (229) |
t0,3{4,3,4} | 4: abbb/bbba | ||
| [4,3,4,2,∞] | or |
{4,4}×t{∞} | |
2: aaaa/bbbb |
| [4,3,4,2,∞] | t1{4,4}×{∞} | |
2: abba/abba | |
| [∞,2,∞,2,∞] | t{∞}×t{∞}×{∞} | |
4: abcd/abcd | |
| [∞,2,∞,2,∞] = [4,(3,4)*] | t{∞}×t{∞}×t{∞} | |
8: abcd/efgh |
Related polytopes and honeycombs
It is related to the regular 4-polytope tesseract, Schläfli symbol {4,3,3}, which exists in 4-space, and only has 3 cubes around each edge. It's also related to the order-5 cubic honeycomb, Schläfli symbol {4,3,5}, of hyperbolic space with 5 cubes around each edge.
It is in a sequence of polychora and honeycomb with octahedral vertex figures.
| {p,3,4} regular honeycombs | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Space | S3 | E3 | H3 | ||||||||
| Form | Finite | Affine | Compact | Paracompact | Noncompact | ||||||
| Name | {3,3,4} |
{4,3,4} |
{5,3,4} |
{6,3,4} |
{7,3,4} |
{8,3,4} |
... {∞,3,4} | ||||
| Image |  |
 |
 |
 |
|||||||
| Cells | {3,3} |
{4,3} |
{5,3} |
{6,3} |
{7,3} |
{8,3} |
{∞,3} | ||||
It in a sequence of regular polytopes and honeycombs with cubic cells.
| {4,3,p} regular honeycombs | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Space | S3 | E3 | H3 | ||||||||
| Form | Finite | Affine | Compact | Paracompact | Noncompact | ||||||
| Name |
{4,3,3} |
{4,3,4} |
{4,3,5} |
{4,3,6} |
{4,3,7} |
{4,3,8} |
... {4,3,∞} | ||||
| Image |  |
 |
 |
 |
|||||||
| Vertex figure |
 {3,3} |
 {3,4} |
 {3,5} |
 {3,6} |
 {3,7} |
 {3,8} |
 {3,∞} | ||||
| {p,3,p} regular honeycombs | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Space | S3 | Euclidean | H3 | ||||||||
| Form | Finite | Affine | Compact | Paracompact | Noncompact | ||||||
| Name | {3,3,3} | {4,3,4} | {5,3,5} | {6,3,6} | {7,3,7} | {8,3,8}... | {∞,3,∞} | ||||
| Image |  |
 |
 |
 |
|||||||
| Cells |  {3,3} |
 {4,3} |
 {5,3} |
 {6,3} |
 {7,3} |
 {8,3} |
 {∞,3} | ||||
| Vertex figure |
 {3,3} |
 {3,4} |
 {3,5} |
 {3,6} |
 {3,7} |
 {3,8} |
 {3,∞} | ||||
Related Euclidean tessellations
The [4,3,4], ![]()
![]()
![]()
![]()
![]()
![]()
![]() , Coxeter group generates 15 permutations of uniform tessellations, 9 with distinct geometry including the alternated cubic honeycomb. The expanded cubic honeycomb (also known as the runcinated tesseractic honeycomb) is geometrically identical to the cubic honeycomb.
, Coxeter group generates 15 permutations of uniform tessellations, 9 with distinct geometry including the alternated cubic honeycomb. The expanded cubic honeycomb (also known as the runcinated tesseractic honeycomb) is geometrically identical to the cubic honeycomb.
| C3 honeycombs | |||||
|---|---|---|---|---|---|
| Space group |
Fibrifold | Extended symmetry |
Extended diagram |
Order | Honeycombs |
| Pm3m (221) |
4−:2 | [4,3,4] | ×1 | ||
| Fm3m (225) |
2−:2 | [1+,4,3,4] ↔ [4,31,1] |
↔ |
Half | |
| I43m (217) |
4o:2 | [[(4,3,4,2+)]] | Half × 2 | ||
| Fd3m (227) |
2+:2 | [[1+,4,3,4,1+]] ↔ [[3[4]]] |
↔ |
Quarter × 2 | |
| Im3m (229) |
8o:2 | [[4,3,4]] | ×2 | ||
The [4,31,1], ![]()
![]()
![]()
![]()
![]() , Coxeter group generates 9 permutations of uniform tessellations, 4 with distinct geometry including the alternated cubic honeycomb.
, Coxeter group generates 9 permutations of uniform tessellations, 4 with distinct geometry including the alternated cubic honeycomb.
| B3 honeycombs | |||||
|---|---|---|---|---|---|
| Space group |
Fibrifold | Extended symmetry |
Extended diagram |
Order | Honeycombs |
| Fm3m (225) |
2−:2 | [4,31,1] ↔ [4,3,4,1+] |
↔ |
×1 | |
| Fm3m (225) |
2−:2 | <[1+,4,31,1]> ↔ <[3[4]]> |
↔ |
×2 | |
| Pm3m (221) |
4−:2 | <[4,31,1]> | ×2 | ||
This honeycomb is one of five distinct uniform honeycombs[2] constructed by the Coxeter group. The symmetry can be multiplied by the symmetry of rings in the Coxeter–Dynkin diagrams:
| A3 honeycombs | ||||||
|---|---|---|---|---|---|---|
| Space group |
Fibrifold | Square symmetry |
Extended symmetry |
Extended diagram |
Extended group |
Honeycomb diagrams |
| F43m (216) |
1o:2 | a1 |
[3[4]] | (None) | ||
| Fm3m (225) |
2−:2 | d2 |
<[3[4]]> ↔ [4,31,1] |
↔ |
×21 ↔ |
|
| Fd3m (227) |
2+:2 | g2 |
[[3[4]]] or [2+[3[4]]] |
↔ |
×22 | |
| Pm3m (221) |
4−:2 | d4 |
<2[3[4]]> ↔ [4,3,4] |
↔ |
×41 ↔ |
|
| I3 (204) |
8−o | r8 |
[4[3[4]]]+ ↔ [[4,3<sup>+</sup>,4]] |
↔ |
½×8 ↔ ½×2 |
|
| Im3m (229) |
8o:2 | [4[3[4]]] ↔ 4,3,4 |
×8 ↔ ×2 |
|||
Rectified cubic honeycomb
| Rectified cubic honeycomb | |
|---|---|
| Type | Uniform honeycomb |
| Cells | Octahedron Cuboctahedron |
| Schläfli symbol | r{4,3,4} or t1{4,3,4} r{3[4]} |
| Coxeter diagrams | |
| Vertex figure | 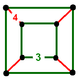 Cuboid |
| Space group Fibrifold notation | Pm3m (221) 4−:2 |
| Coxeter group | , [4,3,4] |
| Dual | oblate octahedrille (Square bipyramidal honeycomb) |
| Properties | vertex-transitive, edge-transitive |
The rectified cubic honeycomb or rectified cubic cellulation is a uniform space-filling tessellation (or honeycomb) in Euclidean 3-space. It is composed of octahedra and cuboctahedra in a ratio of 1:1.
John Horton Conway calls this honeycomb a cuboctahedrille, and its dual oblate octahedrille.


Symmetry
There are four uniform colorings for the cells of this honeycomb with reflective symmetry, listed by their Coxeter group, and Wythoff construction name, and the Coxeter diagram below.
| Symmetry | [4,3,4] |
[1+,4,3,4] [4,31,1], |
[4,3,4,1+] [4,31,1], |
[1+,4,3,4,1+] [3[4]], |
|---|---|---|---|---|
| Space group | Pm3m (221) | Fm3m (225) | Fm3m (225) | F43m (216) |
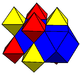
| Coloring | 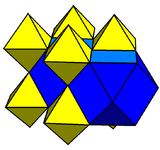 |
 |
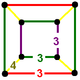
 |
 |
| Coxeter diagram |
||||
| Vertex figure |  |
 |
 |
 |
| Vertex figure symmetry |
D4h [4,2] (*224) order 16 |
D2h [2,2] (*222) order 8 |
C4v [4] (*44) order 8 |
C2v [2] (*22) order 4 |
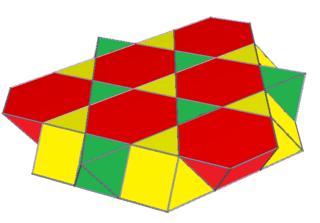
This honeycomb can be divided on trihexagonal tiling planes, using the hexagon centers of the cuboctahedra, creating two triangular cupolae. This scaliform honeycomb is represented by Coxeter diagram ![]()
![]()
![]()
![]()
![]()
![]()
![]() , and symbol s3{2,6,3}, with coxeter notation symmetry [2+,6,3].
, and symbol s3{2,6,3}, with coxeter notation symmetry [2+,6,3].
-
 .
.
Truncated cubic honeycomb
| Truncated cubic honeycomb | |
|---|---|
| Type | Uniform honeycomb |
| Schläfli symbol | t{4,3,4} or t0,1{4,3,4} |
| Coxeter diagrams | |
| Cell type | 3.8.8, {3,4} |
| Face type | {3}, {4}, {8} |
| Vertex figure | 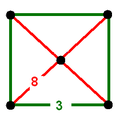 Isosceles square pyramid |
| Space group Fibrifold notation | Pm3m (221) 4−:2 |
| Coxeter group | , [4,3,4] |
| Dual | Pyramidille (Hexakis cubic honeycomb) |
| Properties | vertex-transitive |
The truncated cubic honeycomb or truncated cubic cellulation is a uniform space-filling tessellation (or honeycomb) in Euclidean 3-space. It is composed of truncated cubes and octahedra in a ratio of 1:1.
John Horton Conway calls this honeycomb a truncated cubille, and its dual pyramidille.

Symmetry
There is a second uniform coloring by reflectional symmetry of the Coxeter groups, the second seen with alternately colored truncated cubic cells.
| Construction | Bicantellated alternate cubic | Truncated cubic honeycomb |
|---|---|---|
| Coxeter group | [4,31,1], | [4,3,4], =<[4,31,1]> |
| Space group | Fm3m | Pm3m |
| Coloring |  |
 |
| Coxeter diagram | ||
| Vertex figure |  |
 |
Bitruncated cubic honeycomb
| Bitruncated cubic honeycomb | |
|---|---|
| Type | Uniform honeycomb |
| Schläfli symbol | 2t{4,3,4} or t1,2{4,3,4} |
| Coxeter diagram |
|
| Cell type | (4.6.6) |
| Face types | square {4} hexagon {6} |
| Edge figure | isosceles triangle {3} |
| Vertex figure |  (disphenoid tetrahedron) |
| Space group Fibrifold notation Coxeter notation | Im3m (229) 8o:2 [[4,3,4]] |
| Coxeter group | , [4,3,4] |
| Dual | Oblate tetrahedrille Disphenoid tetrahedral honeycomb |
| Properties | isogonal, isotoxal, isochoric |
The bitruncated cubic honeycomb or bitruncated cubic cellulation is a space-filling tessellation (or honeycomb) in Euclidean 3-space made up of truncated octahedra. It has 4 truncated octahedra around each vertex. Being composed entirely of truncated octahedra, it is cell-transitive. It is also edge-transitive, with 2 hexagons and one square on each edge, and vertex-transitive. It is one of 28 uniform honeycombs.
John Horton Conway calls this honeycomb a truncated octahedrille in his Architectonic and catoptric tessellation list, with its dual called an oblate tetrahedrille, also called a disphenoid tetrahedral honeycomb. Although a regular tetrahedron can not tessellate space alone, this dual has identical disphenoid tetrahedron cells with isosceles triangle faces.
It can be realized as the Voronoi tessellation of the body-centred cubic lattice. Lord Kelvin conjectured that a variant of the bitruncated cubic honeycomb (with curved faces and edges, but the same combinatorial structure) is the optimal soap bubble foam. However, the Weaire–Phelan structure is a less symmetrical, but more efficient, foam of soap bubbles.
Symmetry
The vertex figure for this honeycomb is a disphenoid tetrahedron, and it is also the Goursat tetrahedron (fundamental domain) for the Coxeter group. This honeycomb has four uniform constructions, with the truncated octahedral cells having different Coxeter groups and Wythoff constructions. These uniform symmetries can be represented by coloring differently the cells in each construction.
| Space group | Im3m (229) | Pm3m (221) | Fm3m (225) | F43m (216) | Fd3m (227) |
|---|---|---|---|---|---|
| Fibrifold | 8o:2 | 4−:2 | 2−:2 | 1o:2 | 2+:2 |
| Coxeter group | ×2 [[4,3,4]] =[4[3[4]]] |
[4,3,4] =[2[3[4]]] |
[4,31,1] =<[3[4]]> |
[3[4]] |
×2 [[3[4]]] =[[3[4]]] |
| Coxeter diagram | |||||
| truncated octahedra | 1 |
1:1 |
2:1:1 |
1:1:1:1 |
1:1 |
| Vertex figure |  |
 |
 |
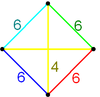 |
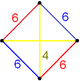 |
| Vertex figure symmetry |
[2+,4] (order 8) |
[2] (order 4) |
[ ] (order 2) |
[ ]+ (order 1) |
[2]+ (order 2) |
| Image Colored by cell |
 |
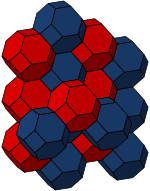 |
 |
 |
 |
Projection by folding
The bitruncated cubic honeycomb can be orthogonally projected into the planar truncated square tiling by a geometric folding operation that maps two pairs of mirrors into each other. The projection of the bitruncated cubic honeycomb creating two offset copies of the truncated square tiling vertex arrangement of the plane:
| Coxeter group |
||
|---|---|---|
| Coxeter diagram |
||
| Graph | 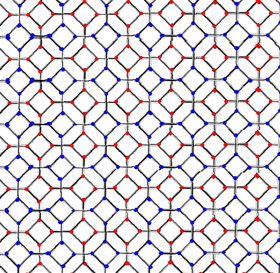 Bitruncated cubic honeycomb |
 Truncated square tiling |
Alternated bitruncated cubic honeycomb
| Alternated bitruncated cubic honeycomb | |
|---|---|
| Type | Uniform honeycomb |
| Schläfli symbol | 2s{4,3,4} |
| Coxeter diagrams | |
| Cells | tetrahedron icosahedron |
| Vertex figure |  |
| Coxeter group | [4,3,4], |
| Properties | vertex-transitive |
The alternated bitruncated cubic honeycomb or bisnub cubic honeycomb can be creating regular icosahedron from the truncated octahedra with irregular tetrahedral cells created in the gaps. There are three constructions from three related Coxeter diagrams: ![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
, ![]()
![]()
![]()
![]()
![]() , and
, and ![]()
![]()
![]()
![]()
![]() . These have symmetry [4,3+,4], [4,(31,1)+] and [3[4]]+ respectively. The first and last symmetry can be doubled as [[4,3+,4]] and [[3[4]]]+.
. These have symmetry [4,3+,4], [4,(31,1)+] and [3[4]]+ respectively. The first and last symmetry can be doubled as [[4,3+,4]] and [[3[4]]]+.
This honeycomb is represented in the boron atoms of the α-rhombihedral crystal. The centers of the icosahedra are located at the fcc positions of the lattice.[3]
| Space group | I3 (204) | Pm3 (200) | Fm3 (202) | Fd3 (203) | F23 (196) |
|---|---|---|---|---|---|
| Fibrifold | 8−o | 4− | 2− | 2o+ | 1o |
| Coxeter group | [[4,3+,4]] | [4,3+,4] | [4,(31,1)+] | [[3[4]]]+ | [3[4]]+ |
| Coxeter diagram | |||||
| Order | double | full | half | quarter double |
quarter |
Cantellated cubic honeycomb
| Cantellated cubic honeycomb | |
|---|---|
| Type | Uniform honeycomb |
| Schläfli symbol | rr{4,3,4} or t0,2{4,3,4} |
| Coxeter diagram | |
| Cells | rr{4,3} r{4,3} {4,3} |
| Vertex figure |  (Wedge) |
| Space group Fibrifold notation | Pm3m (221) 4−:2 |
| Coxeter group | [4,3,4], |
| Dual | quarter oblate octahedrille |
| Properties | vertex-transitive |
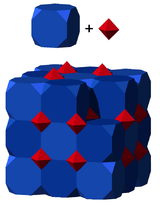
The cantellated cubic honeycomb or cantellated cubic cellulation is a uniform space-filling tessellation (or honeycomb) in Euclidean 3-space. It is composed of rhombicuboctahedra, cuboctahedra, and cubes in a ratio of 1:1:3.
John Horton Conway calls this honeycomb a 2-RCO-trille, and its dual quarter oblate octahedrille.
Images
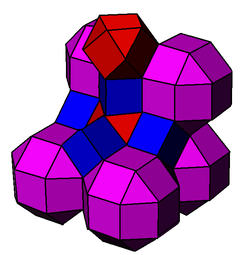 |
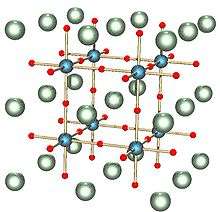 It is closely related to the perovskite structure, shown here with cubic symmetry, with atoms placed at the center of the cells of this honeycomb. |
Symmetry
There is a second uniform colorings by reflectional symmetry of the Coxeter groups, the second seen with alternately colored rhombicuboctahedral cells.
| Construction | Truncated cubic honeycomb | Bicantellated alternate cubic |
|---|---|---|
| Coxeter group | [4,3,4], =<[4,31,1]> |
[4,31,1], |
| Space group | Pm3m | Fm3m |
| Coxeter diagram | ||
| Coloring |  |
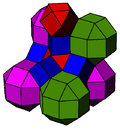 |
| Vertex figure |  |
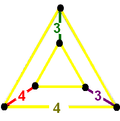 |
| Vertex figure symmetry |
[ ] order 2 |
[ ]+ order 1 |
Cantitruncated cubic honeycomb
| Cantitruncated cubic honeycomb | |
|---|---|
| Type | Uniform honeycomb |
| Schläfli symbol | tr{4,3,4} or t0,1,2{4,3,4} |
| Coxeter diagram | |
| Vertex figure | 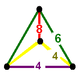  (Irreg. tetrahedron) |
| Coxeter group | [4,3,4], |
| Space group Fibrifold notation | Pm3m (221) 4−:2 |
| Dual | triangular pyramidille |
| Properties | vertex-transitive |
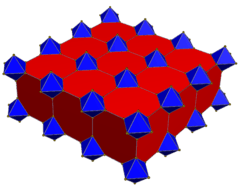
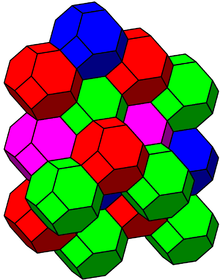
The cantitruncated cubic honeycomb or cantitruncated cubic cellulation is a uniform space-filling tessellation (or honeycomb) in Euclidean 3-space, made up of truncated cuboctahedra, truncated octahedra, and cubes in a ratio of 1:1:3.
John Horton Conway calls this honeycomb a n-tCO-trille, and its dual triangular pyramidille.
Images
Four cells exist around each vertex:
Related polyhedra and honeycombs
It is related to a skew apeirohedron with vertex configuration 4.4.6.6, with the octagons and some of the squares removed. It can be seen as constructed by augmenting truncated cuboctahedral cells, or by augmenting alternated truncated octahedra and cubes.
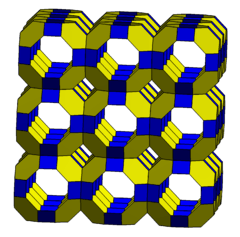 |
 |
Symmetry
Cells can be shown in two different symmetries. The linear Coxeter diagram form can be drawn with one color for each cell type. The bifurcating diagram form can be drawn with two types (colors) of truncated cuboctahedron cells alternating.
| Construction | Cantitruncated cubic | Omnitruncated alternate cubic |
|---|---|---|
| Coxeter group | [4,3,4], =<[4,31,1]> |
[4,31,1], |
| Space group | Pm3m (221) | Fm3m (225) |
| Fibrifold | 4−:2 | 2−:2 |
| Coloring |  |
 |
| Coxeter diagram | ||
| Vertex figure |  |
 |
| Vertex figure symmetry |
[ ] order 2 |
[ ]+ order 1 |
Alternated cantitruncated cubic honeycomb
| Alternated cantitruncated cubic honeycomb | |
|---|---|
| Type | Convex honeycomb |
| Schläfli symbol | sr{4,3,4} sr{4,31,1} |
| Coxeter diagrams | |
| Cells | tetrahedron pseudoicosahedron snub cube |
| Vertex figure |  |
| Coxeter group | [4,31,1], |
| Dual | square quarter pyramidille |
| Properties | vertex-transitive |
The alternated cantitruncated cubic honeycomb or snub rectified cubic honeycomb contains three types of cells: snub cubes, icosahedra (snub tetrahedron), and tetrahedra. In addition the gaps created at the alternated vertices form tetrahedral cells.
Although it is not uniform, constructionally it can be given as Coxeter diagrams ![]()
![]()
![]()
![]()
![]() or
or ![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Runcic cantitruncated cubic honeycomb
| Runcic cantitruncated cubic honeycomb | |
|---|---|
| Type | Convex honeycomb |
| Schläfli symbol | sr3{4,3,4} |
| Coxeter diagrams | |
| Cells | rhombicuboctahedron snub cube cube |
| Vertex figure | |
| Coxeter group | [4,3,4], |
| Dual | |
| Properties | vertex-transitive |
The runcic cantitruncated cubic honeycomb or runcic cubic cellulation contains cells: snub cubes, rhombicuboctahedrons, and cubes. In addition the gaps created at the alternated vertices form an irregular cell.
Although it is not uniform, constructionally it can be given as Coxeter diagram ![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Runcitruncated cubic honeycomb
| Runcitruncated cubic honeycomb | |
|---|---|
| Type | Uniform honeycomb |
| Schläfli symbol | t0,1,3{4,3,4} |
| Coxeter diagrams | |
| Cells | rhombicuboctahedron truncated cube octagonal prism cube |
| Vertex figure |  (Trapezoidal pyramid) |
| Coxeter group | [4,3,4], |
| Space group Fibrifold notation | Pm3m (221) 4−:2 |
| Dual | square quarter pyramidille |
| Properties | vertex-transitive |
The runcitruncated cubic honeycomb or runcitruncated cubic cellulation is a uniform space-filling tessellation (or honeycomb) in Euclidean 3-space. It is composed of rhombicuboctahedra, truncated cubes, octagonal prisms, and cubes in a ratio of 1:1:3:3.
Its name is derived from its Coxeter diagram, ![]()
![]()
![]()
![]()
![]()
![]()
![]() with three ringed nodes representing 3 active mirrors in the Wythoff construction from its relation to the regular cubic honeycomb.
with three ringed nodes representing 3 active mirrors in the Wythoff construction from its relation to the regular cubic honeycomb.
John Horton Conway calls this honeycomb a 1-RCO-trille, and its dual square quarter pyramidille.

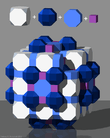
A related uniform skew apeirohedron exists with the same vertex arrangement, but some of the square and all of the octagons removed. It can be seen as truncated tetrahedra and truncated cubes augmented together.
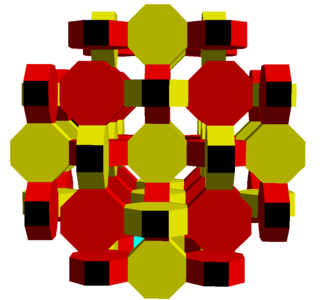
Omnitruncated cubic honeycomb
| Omnitruncated cubic honeycomb | |
|---|---|
| Type | Uniform honeycomb |
| Schläfli symbol | t0,1,2,3{4,3,4} |
| Coxeter diagram | |
| Vertex figure |  Phyllic disphenoid |
| Space group Fibrifold notation Coxeter notation | Im3m (229) 8o:2 [[4,3,4]] |
| Coxeter group | [4,3,4], |
| Dual | eighth pyramidille |
| Properties | vertex-transitive |
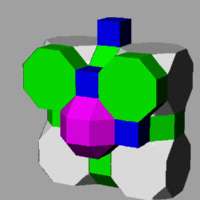
The omnitruncated cubic honeycomb or omnitruncated cubic cellulation is a uniform space-filling tessellation (or honeycomb) in Euclidean 3-space. It is composed of truncated cuboctahedra and octagonal prisms in a ratio of 1:3.
John Horton Conway calls this honeycomb a b-tCO-trille, and its dual eighth pyramidille.
Symmetry
Cells can be shown in two different symmetries. The Coxeter diagram form has two colors of truncated cuboctahedra and octahedral prisms. The symmetry can be doubled by relating the first and last branches of the Coxeter diagram, which can be shown with one color for all the truncated cuboctahedral and octahedral prism cells.
| Symmetry | , [4,3,4] | ×2, 4,3,4 |
|---|---|---|
| Space group | Pm3m (221) | Im3m (229) |
| Fibrifold | 4−:2 | 8o:2 |
| Coloring |  |
 |
| Coxeter diagram | ||
| Vertex figure |  |
 |
Related polyhedra
Two related uniform skew apeirohedron exist with the same vertex arrangement. The first has octagons removed, and vertex configuration 4.4.4.6. It can be seen as truncated cuboctahedra and octagonal prisms augmented together. The second can be seen as augmented octagonal prisms.
4.4.4.6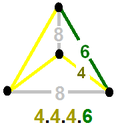 |
4.8.4.8 |
|---|---|
 |
 |
Alternated omnitruncated cubic honeycomb
| Alternated omnitruncated cubic honeycomb | |
|---|---|
| Type | Uniform honeycomb |
| Schläfli symbol | ht0,1,2,3{4,3,4} |
| Coxeter diagram | |
| Cells | snub cube square antiprism tetrahedron |
| Vertex figure |  |
| Symmetry | [[4,3,4]]+ |
| Properties | vertex-transitive |
A alternated omnitruncated cubic honeycomb or full snub cubic honeycomb can be constructed by alternation of the omnitruncated cubic honeycomb, although it can not be made uniform, but it can be given Coxeter diagram: ![]()
![]()
![]()
![]()
![]()
![]()
![]() and has symmetry [[4,3,4]]+. It makes snub cubes from the truncated cuboctahedra, square antiprisms from the octagonal prisms and with new tetrahedral cells created in the gaps.
and has symmetry [[4,3,4]]+. It makes snub cubes from the truncated cuboctahedra, square antiprisms from the octagonal prisms and with new tetrahedral cells created in the gaps.
Truncated square prismatic honeycomb
| Truncated square prismatic honeycomb | |
|---|---|
| Type | Uniform honeycomb |
| Schläfli symbol | t{4,4}×{∞} or t0,1,3{4,4,2,∞} tr{4,4}×{∞} or t0,1,2,3{4,4,∞} |
| Coxeter-Dynkin diagram | |
| Coxeter group | [4,4,2,∞] |
| Dual | Tetrakis square prismatic tiling |
| Properties | vertex-transitive |
The truncated square prismatic honeycomb or tomo-square prismatic cellulation is a space-filling tessellation (or honeycomb) in Euclidean 3-space. It is composed of octagonal prisms and cubes in a ratio of 1:1.

It is constructed from a truncated square tiling extruded into prisms.
It is one of 28 convex uniform honeycombs.
Snub square prismatic honeycomb
| Snub square prismatic honeycomb | |
|---|---|
| Type | Uniform honeycomb |
| Schläfli symbol | s{4,4}×{∞} sr{4,4}×{∞} |
| Coxeter-Dynkin diagram | |
| Coxeter group | [4+,4,2,∞] [(4,4)+,2,∞] |
| Dual | Cairo pentagonal prismatic honeycomb |
| Properties | vertex-transitive |
The snub square prismatic honeycomb or simo-square prismatic cellulation is a space-filling tessellation (or honeycomb) in Euclidean 3-space. It is composed of cubes and triangular prisms in a ratio of 1:2.

It is constructed from a snub square tiling extruded into prisms.
It is one of 28 convex uniform honeycombs.
See also
| Wikimedia Commons has media related to Cubic honeycomb. |
- Architectonic and catoptric tessellation
- Alternated cubic honeycomb
- List of regular polytopes
- Order-5 cubic honeycomb A hyperbolic cubic honeycomb with 5 cubes per edge
References
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, (2008) The Symmetries of Things, ISBN 978-1-56881-220-5 (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, Architectonic and Catoptric tessellations, p 292-298, includes all the nonprismatic forms)
- Coxeter, H.S.M. Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8 p. 296, Table II: Regular honeycombs
- George Olshevsky, Uniform Panoploid Tetracombs, Manuscript (2006) (Complete list of 11 convex uniform tilings, 28 convex uniform honeycombs, and 143 convex uniform tetracombs)
- Branko Grünbaum, Uniform tilings of 3-space. Geombinatorics 4(1994), 49 - 56.
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10] (1.9 Uniform space-fillings)
- A. Andreini, Sulle reti di poliedri regolari e semiregolari e sulle corrispondenti reti correlative (On the regular and semiregular nets of polyhedra and on the corresponding correlative nets), Mem. Società Italiana della Scienze, Ser.3, 14 (1905) 75–129.
- Klitzing, Richard. "3D Euclidean Honeycombs x4o3o4o - chon - O1".
- Uniform Honeycombs in 3-Space: 01-Chon
| Fundamental convex regular and uniform honeycombs in dimensions 3–10 (or 2-9) | |||||
|---|---|---|---|---|---|
| Family | / / | ||||
| Uniform tiling | {3[3]} | δ3 | hδ3 | qδ3 | Hexagonal |
| Uniform convex honeycomb | {3[4]} | δ4 | hδ4 | qδ4 | |
| Uniform 5-honeycomb | {3[5]} | δ5 | hδ5 | qδ5 | 24-cell honeycomb |
| Uniform 6-honeycomb | {3[6]} | δ6 | hδ6 | qδ6 | |
| Uniform 7-honeycomb | {3[7]} | δ7 | hδ7 | qδ7 | 222 |
| Uniform 8-honeycomb | {3[8]} | δ8 | hδ8 | qδ8 | 133 • 331 |
| Uniform 9-honeycomb | {3[9]} | δ9 | hδ9 | qδ9 | 152 • 251 • 521 |
| Uniform 10-honeycomb | {3[10]} | δ10 | hδ10 | qδ10 | |
| Uniform n-honeycomb | {3[n]} | δn | hδn | qδn | 1k2 • 2k1 • k21 |